最も有名な巻取モデルがHakielモデルである。このモデルの根本になっている関係式の導出が巻取理論の本質の理解につながる。

Hakielモデルの基礎方程式

Hakielモデルのもとになっている4つの関係式

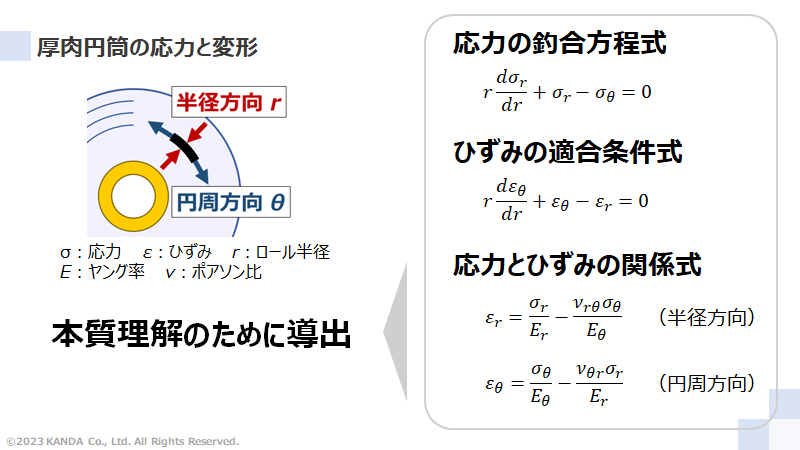
半径方向ヤング率の非線形性を考慮した理論モデルをHakiel氏が提示した。これが今日における巻取理論のベースになっており、Hakielモデルと呼ばれている。このモデルの基礎方程式は次式で表される。

この方程式は厚肉円筒に関する4つの式を整理して得られる。記号の意味は図を参照。

（応力の釣合方程式）

（ひずみの適合条件式）

（応力とひずみの関係式）

「応力の釣合方程式」と「ひずみの適合条件式」のそれぞれ自体を導出すること、これが巻取理論の本質を理解するのに役立つ。

応力の釣合方程式の導出

内外圧を受ける厚肉円筒の"応力"を考える

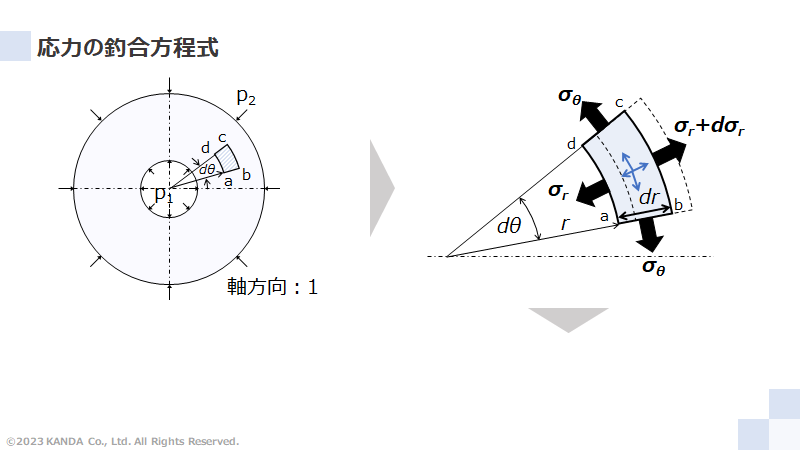
内圧p₁と外圧p₂が作用した軸方向が1の厚肉円筒内の微小要素abcdを切り出す。極座標（r, θ）をとると、微小要素に作用する応力は半径方向応力σ_rと円周方向応力σ_θである。

微小要素の4つの面に作用する力はそれぞれ以下のように表される。

（面ab）

（面bc）

（面cd）

（面da）

以上の式より、半径方向（r方向）の力の釣り合いは

となる。さらに整理すると

となって最終的に応力の釣合方程式が次のように導出される。

以上のプロセスより、この応力の釣合方程式は半径方向に対する一次元の関係を表していることがわかる。

ひずみの適合条件式の導出

内外圧を受ける厚肉円筒の"変形"を考える

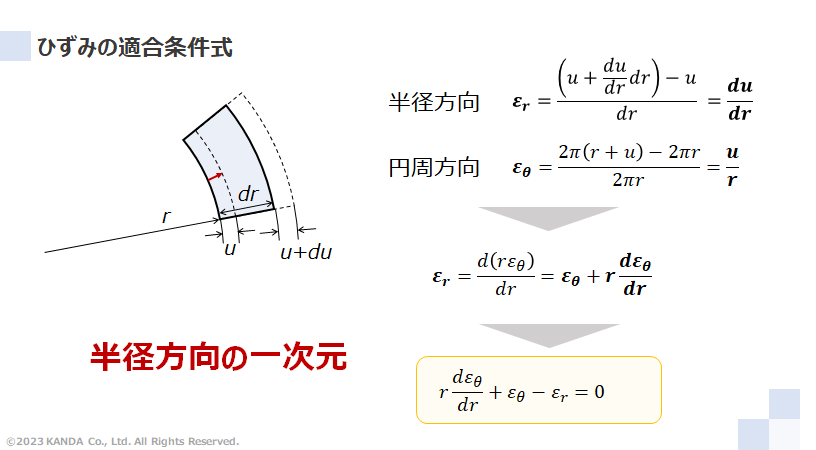
微小要素が内外圧によって変形し、実線から破線の位置に変位した状態を想定する。半径rでの変位をuとすれば、半径r+drでの変位はu+(du/dr)drとなる。そうすると半径方向ひずみε_rと円周方向ひずみε_θはそれぞれ次のように表される。

（半径方向）

（円周方向）

半径ひずみε_rに円周方向ε_θを代入すると

となり、最終的にひずみの適合条件式が次のように導出される。

以上のプロセスより、ひずみの適合条件式もまた半径方向に対する一次元の関係を表していることがわかる。

Hakielモデルにおける仮定との関係

理論を使うにはその仮定はもちろんのこと、実際との違いも理解しなければならない。理解を怠ると誤った結果につながる

内外圧を受ける厚肉円筒の応力と変形から導出された関係式がHakielモデルのベースになっている。このモデルは半径方向に対する一次元の関係を表したものである。厚肉円筒ではなく巻取ロールで考えるとHakiel氏が提示した下記項目が巻取理論の仮定になる。なお、本技術情報で関係する仮定のみ抜粋している。

1. 巻取ロールは完全な円筒形状であり、ロール内はウェブの厚さ、幅、表面粗さなどは均一とする。
2. ウェブはスパイラル状ではなく、引っ張られた薄肉円筒の積み重ねで表現される。また、単一の薄肉円筒における弾性特性は一定とする。
3. 巻取ロールの内部応力は半径方向位置の関数で表現され、円周方向位置と幅方向位置によらない。
4. 平面応力状態を仮定とし、軸方向応力はゼロとする。

Hakielモデルとこれを基礎に高度化したモデルは上記仮定のもとで成立する。したがって完全な円筒形状でなかったり、円周方向や幅方向でウェブ物性が変化したりする場合には別途考察する必要がある。仮定から外れる現象は実際の生産現場ではたびたび見受けられる。この点については経験で補ってやる必要がある。

参考書籍

渋谷寿一, 本間寛臣, 斎藤憲司, “現代材料力学” 朝倉書店, 2004

関連ページ

巻取りの基礎理論 – Hakielモデルでの数値計算とその概念

ロール品質を数値化する理論モデルの歴史