ウェブは張力が作用した状態で巻き取られる。この張力は巻取方向(いわゆるMD:Machine Direction)に作用し、この力によってウェブは変形して伸びる。ウェブが力によって変形した際に、元に戻ろうとする強さ(弾性)を引張ヤング率という指標で評価する。ここでは、引張ヤング率を算出するプロセスを具体的に紹介する。なお、巻取理論における円周方向ヤング率とは、引張ヤング率のことを指している。
材料力学の基礎「応力とひずみとヤング率」について
引張ヤング率を評価するベースである材料力学について、その基礎である「応力」と「ひずみ」と「ヤング率」を説明する。
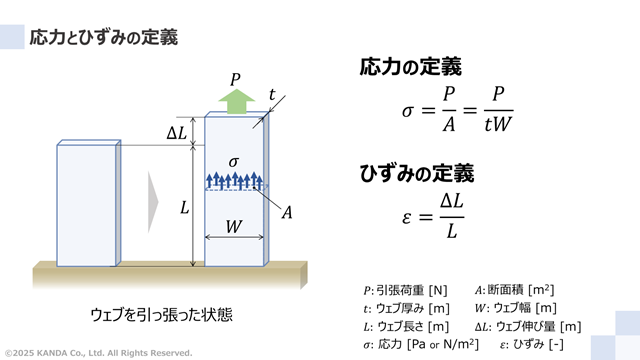
長さL[m]のウェブに引張荷重P[N]が作用し、鉛直方向に伸び量ΔL[m]だけ変形した状態を図に示している。なお、ウェブの厚みをt[m]、幅をW[m] 、断面積をA[m2]で表している。外力が作用して変形する固体の挙動を取り扱う材料力学では、“外力と変形”を寸法によらないように一般化した”応力とひずみ”で表現する。
ウェブを引張荷重Pで引っ張ったときに、その断面Aに一様な力が分布すると考える。この一様な力を合わせるとPに等しい。このとき、単位面積当たりの力を応力σと呼び、次式で与えられる。
![]()
ここで、応力の単位は式(1)から[N/m2]であるが、パスカル[Pa]でも表される。
一方、材料に荷重Pが加わると変形して伸びる。このときの伸び量ΔLを元の長さLで割った値をひずみεと呼び、次のように定義される。
![]()
ここで、ひずみの単位は式(2)から[m/m]であり、無次元量[-]で表される。ひずみは元のサイズに対する伸び量の割合を意味している。
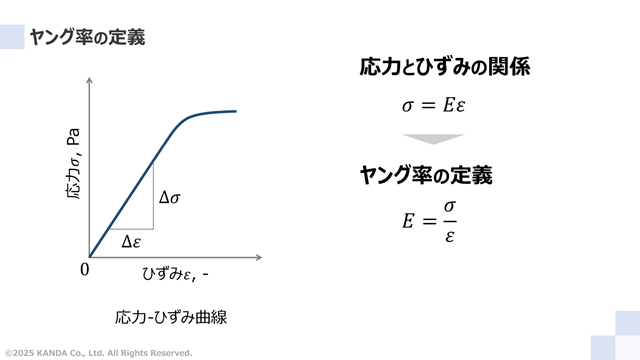
引張試験で計測した荷重と伸び量を式(1)と式(2)にそれぞれ代入すると、応力とひずみの値が計算できる。これらのデータをグラフ化すると、図のように応力‐ひずみ曲線を描くことができる。このとき、応力とひずみの関係に比例定数(傾き)Eをもちいると、次のように表される。
![]()
比例定数Eは材料固有の値である。いくつかの名称があるが、ここではヤング率という名称を使う。式(3)より、ヤング率は次式で与えられる。なお、単位は[Pa]が一般的である。
![]()
引張試験とその実例データ
引張試験の方法について説明し、あるプラスチックフィルムをもちいた試験データの実例を示す。
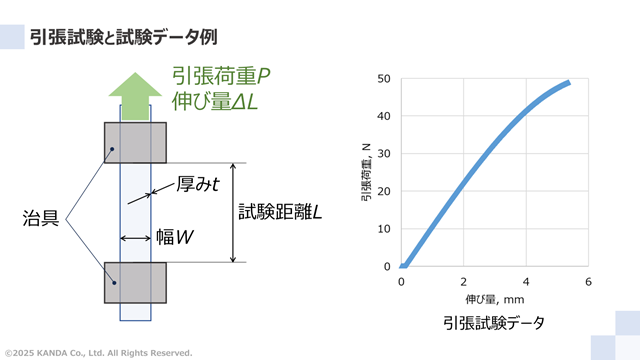
引張試験に用いられる万能材料試験機には、サンプルを固定する二つの治具と、その片方に力を計測するロードセルが取り付けられている。
試験準備として、長手方向が試験方向になるように短冊状にサンプルをカットし、その両端を治具によって固定する。ここで、サンプルの幅と厚みをそれぞれW[m]とt[m]、固定したときの治具間の距離(試験距離)をL[m]とする。
試験中は、治具間の距離を増大させることで変化するサンプルの伸び量ΔL[m]と引張荷重P[N]のデータを随時取得する。治具間距離の増大量とサンプルの伸び量は等しいとして考える。
ある二軸延伸ポリエチレンテレフタレートフィルムを用いて引張試験をおこなった。取得した伸び量と引張荷重のデータをもとに作成したグラフに示している。ここで、この結果は試験に用いたポリエチレンテレフタレート(PET)フィルム固有のものであり、すべてのPETフィルムを代表するものではない。プラスチックフィルムの引張ヤング率は原材料、製膜や延伸倍率といった製造条件などの様々な影響を受けることが知られている。その他の分類のウェブ※であっても同様のことがいえる。
※紙、金属箔、織布・不織布、異種材料を貼合したウェブや表面塗工したウェブといった複合ウェブなど
試験条件としてサンプル幅を10mm、試験距離を200mm、治具間距離の増大速度を0.2mm/sec、データ取得時間を0.01sec/データとした。サンプルの厚みは実測したところ49.8μmであった。なお、試験中は伸び量と引張荷重の傾きに着目し、傾きが直線の線形から徐々に低下する非線形に変化したところで終了させた。取得したデータ点数は結果的に3000程度であった。
試験データから応力とひずみを計算
引張試験で取得した引張荷重と伸び量のデータから、応力とひずみの値をそれぞれ計算する。
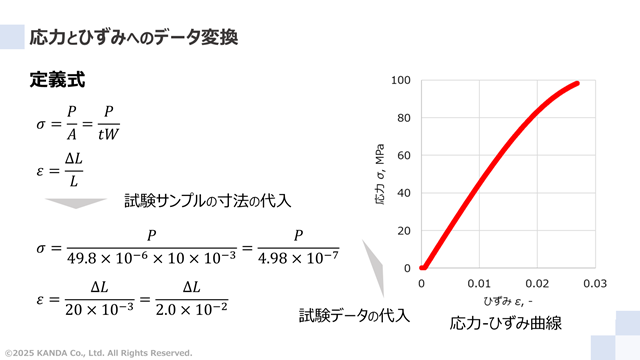
式(1)の応力σの定義式および式(2)のひずみεの定義式の試験サンプルの寸法を代入すると、それぞれ次のように表される。なお、代入する数値は[m]に換算する。試験サンプルの厚みt=49.8μm=49.8×10-6m、幅W=10mm=10×10-3m、試験距離L=200mm=20×10-3mとなる。
![]()
![]()
これらの式に引張試験で取得したデータの引張荷重Pとサンプルの伸び量ΔLを代入すれば、応力σとひずみεの値がそれぞれ算出される。この結果から作成した応力-ひずみ曲線のグラフを図中に示している。
初期値に対するデータ処理
試験初期のデータは必要に応じて処理し、ゼロ点を補正する必要がある。
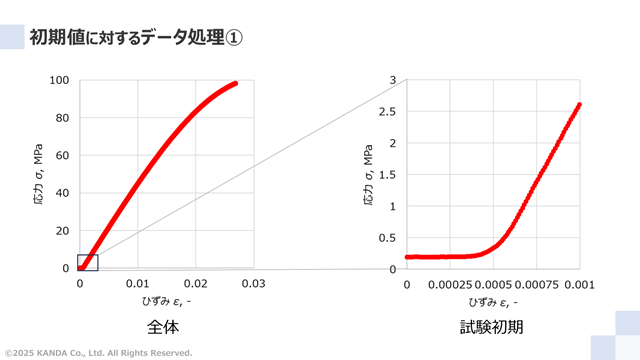
左図は上述した応力-ひずみ曲線であり、右図はひずみ範囲0~0.001(0~0.1%)に着目した試験初期のデータである。後者のグラフは、「ひずみ0のときに応力が0であり、はじめの部分では応力とひずみが直線関係を示す」と専門書などで記載される範囲である。しかし、実際にはそのようになっておらず、理想から乖離している2つの現象が確認できる。
現象①:ひずみが0~0.0003(0~0.03%)の範囲で応力が0.2MPaで一定となっている
現象②:ひずみが0.0005(0.05%)付近における応力の立ち上がりが直線ではなく、曲線になっている
引張試験の状況から、これらの現象は以下の要因ことが関係している可能性がある。
現象①について、サンプルを治具で挟んだ結果として若干のタルミがあったこと、荷重を計測するロードセルのゼロ点調整が不十分であったことの2点である。現象②について、サンプルを固定したときのサンプルや治具の状態が不適切な場合に生じやすい。例えば、サンプルにねじれや片タルミがある、治具がねじれているといったことが挙げられる。理想的な実験値を得るためには、理想的な状態で試験できるように意識するとよいであろう。
次に現象①について、試験後でも対処できる補正のデータ処理を行う。
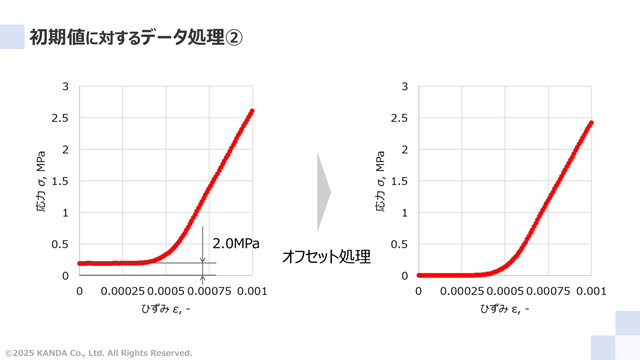
左図の応力の不十分であったゼロ点調整分0.2MPaについて、これを差し引いた結果を右図に示している。
次に、ひずみのゼロ点補正を行う。
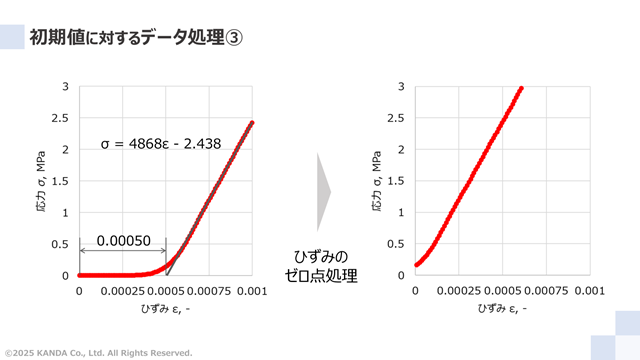
左図は、応力とひずみが直線関係と考えられる、ひずみ範囲が0.0006~0.001のデータを直線近似した結果を示している。
![]()
式(7)より、応力σが0になるひずみεを算出すると0.00050となった。この値を差し引いた結果を右図に示している。これより、応力とひずみのゼロ点調整の不十分であったことへの改善がなされた。
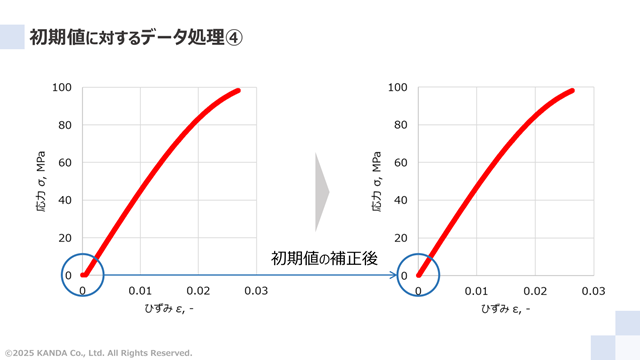
初期値のデータ処理前後のグラフを左図と右図に示している。これより、より理想的な状態に加工できたといえよう。
一般的な方法による引張ヤング率の算出
引張ヤング率は、所定のひずみ範囲における直線近似の傾きから算出される。
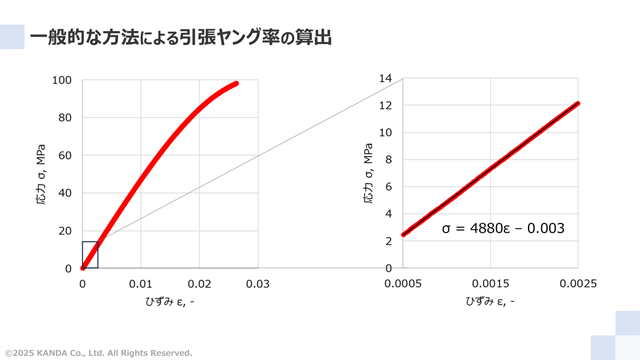
初期値のデータ処理後の応力-ひずみ曲線に対して式(4)を適用すれば、引張ヤング率を算出することができる。ヤング率はひずみに対する応力の傾きであるため、所定の範囲で直線近似したときの係数を求めればよい。
例えば、JISK7161-1「プラスチック-引張特性の求め方-」に記載のある0.0005(0.05%)~0.0025(0.25%)のひずみ範囲を適用した場合、引張ヤング率は4880MPa(=4.88×109Pa)と決定される。
ウェブの受ける刺激を考慮した引張ヤング率の算出
ウェブには張力が作用する。したがって、応力よりも張力に相当する荷重で考える方が直接的であろう。
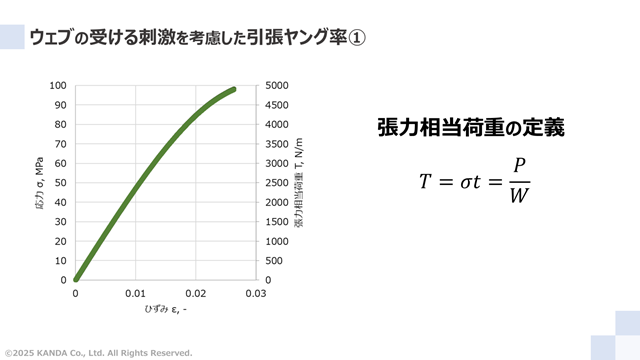
図は初期値のデータ処理後の応力-ひずみ曲線に、張力相当荷重を第2軸に加えたものである。張力相当荷重Tは次式のように応力σにサンプル厚みtをかけた値、あるいは引張荷重Pをサンプル幅Wでわった値で定義する。
![]()
ここで、張力相当荷重の単位は [N/m]である。
試験結果を全体でみると、本試験では5000N/mまでの張力範囲を評価していることに等しい。
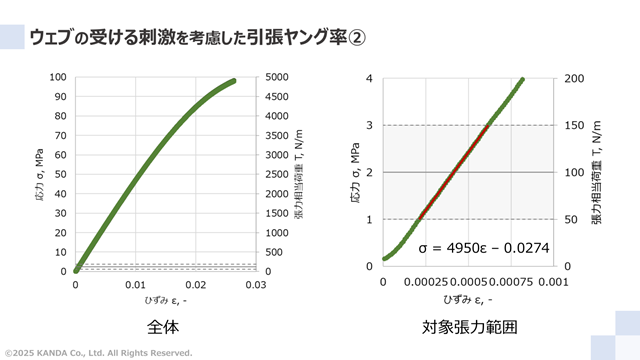
現実の生産における搬送や巻取の張力が100N/mであるとすれば、その張力にみあう張力相当荷重の近傍のデータをもちいる方が理にかなっているであろう。そこで、張力相当荷重が50~150N/m範囲の応力とひずみのデータを引張ヤング率の算出にもちいることにする。
直線近似した結果、引張ヤング率は4950MPa(=4.95×109Pa)となった。これは上述した一般的なひずみの範囲で算出した値とほぼ一致する(1.4%の差)。
引張ヤング率の張力依存性
引張ヤング率を一定とみなしてよいとは限らない。巻取りの条件や状況によっては張力の依存性を考慮した方がよい。
巻取り中のテーパ設定を含め、巻取張力はウェブ製品ごとに適正な値が設定される。そのため、想定される張力範囲の引張ヤング率を把握しておくことが好ましい。特に、ウェブの厚みムラを考慮した理論モデルを用いる場合には重要である。このモデルでは幅方向の張力分布を計算する。ウェブが厚い位置では設定張力以上、薄い位置では設定張力以下になる。条件にもよるが、ウェブ厚薄によって幅位置の張力が設定張力より1桁大きくも小さくもなることがある。
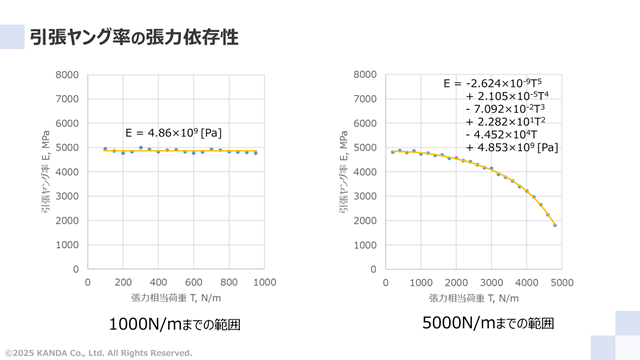
2つの図は張力相当荷重に対する引張ヤング率の関係を示したものである。左図は1000N/mまで、右図は5000N/mまでの張力相当荷重範囲でグラフを作成している。青プロットは張力範囲を基準とした計算値、赤線は平均値あるいは近似値を示している。
左図では、引張ヤング率は張力相当荷重によらず一定とみなせる。平均値は4860MPaであり、計算値との差は±2%であった。つまり、1000N/mまでは、引張ヤング率は4860MPa(=4.86×109Pa)とみなしてよいだろう。
一方、5000N/mまでの張力範囲で考えると、1000N/mの結論とは異なってくる。張力相当荷重が大きくなると、引張ヤング率が低下していく傾向にある。なお、近似値は5次の多項式近似した結果である。この近似次数は計算値をもっとも精度よく近似できた数であり、近似値と計算値の差は±3%であった。
これより、理論計算に適用する引張ヤング率は、張力が1000N/m以下であれば4860MPa、1000N/mを超えることが想定されていれば次の近似式を設定すればよい。
![]()
もし、ウェブ厚みムラの理論モデルを用いる可能性があるならば、この近似式をもちいる方が無難であろう。
各種ウェブの引張ヤング率
PETフィルム以外のウェブについて、その引張ヤング率の張力依存性を紹介する。
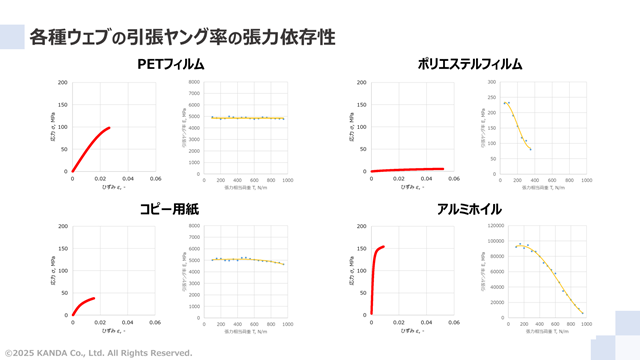
PETフィルムに加え、ポリエステルフィルム、コピー用紙、アルミホイルの応力-ひずみ曲線および引張ヤング率の張力相当荷重依存性の結果をそれぞれ示している。なお、各ウェブはある特定のウェブであり、同じ分類や製品を代表するものではない。
応力-ひずみ曲線のグラフでは応力とひずみの範囲はいずれも同じにしている。一方、引張ヤング率の張力相当荷重依存性のグラフでは、X軸の張力相当荷重は共通の0~1000N/mとしているが、Y軸の引張ヤング率は共通ではない。
これらの結果より、ポリエステルフィルムとコピー用紙とアルミホイルは、張力相当荷重が大きくなると引張ヤング率は低下傾向にあることがわかる。ロール品質をより高精度に理論予測するには、巻取モデルに適用する引張ヤング率はその張力依存性を考慮した方がよいであろう。
近似値の落とし穴と対処例
近似式をもちいる場合、近似範囲外の引張ヤング率の近似値は予期しない値になることがある。
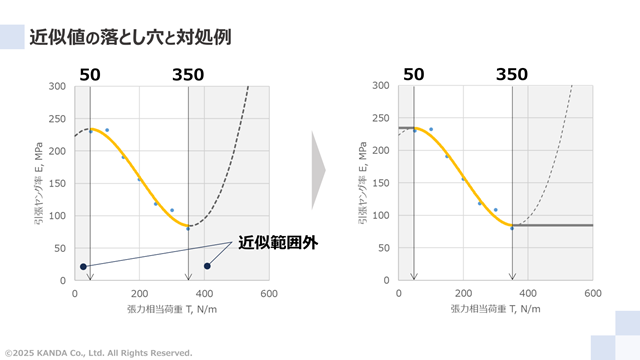
左図は上述したポリエステルフィルムの引張ヤング率の張力依存性の結果に、近似範囲外の近似値(黒の破線)を追加したものである。近似範囲外とは近似対象のデータよりも外側にある範囲のことを指し、ここでは50N/m以下と350N/m以上の範囲になる。なお、近似値はプロットの試験データを3次の多項式近似した近似式から算出している。
近似範囲外の値について、50N/m以下では低下傾向、350N/m以上では上昇傾向にあることがわかる。これはポリエステルフィルムの特性を考えると現実的ではない。理論計算では、このような外挿近似を見逃してしまうことがある。これを回避する方法を2つ挙げる。
- 実験的に広範囲の引張ヤング率を取得する。
- 数値計算上で外挿近似になったら特定の値に固定する。
2つ目の方法を適用した結果を右図に示している。張力が50N/m以下の場合、近似式に50N/mの値を代入した引張ヤング率の値を採用する。式350N/m以上の場合でも同様とする。その結果、図中の黒直線のように調整され、外挿近似による明らかな理論予測の精度低下を抑えられる。
複合ウェブの引張ヤング率
異種材料を貼合したウェブや塗工層を設けたウェブといった複合ウェブについて、その引張ヤング率の算出について紹介する。
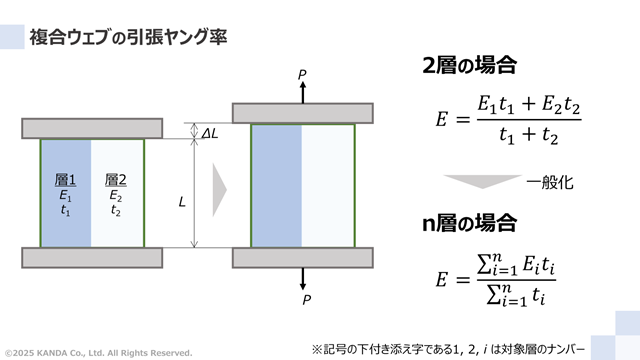
層1と層2からなる複合ウェブを例に、試験距離Lで力Pが作用したときに伸び量ΔLが生じた状態を図に示している。なお、ウェブ同士の貼り合わせであればウェブ、塗工したウェブであれば塗工層とウェブのように層を考えればよい。このような複合ウェブの引張ヤング率は、次の方法で算出できる。
方法1:複合ウェブのまま引張試験をおこなって引張ヤング率を算出する。上述したPETフィルムの場合と同じ方法であり、簡便な方法といえる。
方法2:層ごとに引張試験をおこなってそれぞれの引張ヤング率を算出する。その後、各層の引張ヤング率と厚みを次式に代入して複合ウェブの引張ヤング率を計算する。
![]()
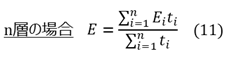
ここで式(11)のn層とは、n=1, 2, 3・・・と多層の複合ウェブに対応させた表現であり、一般化した意味を持っている。
次に方法2の具体例として、層1をPETフィルム、層2をポリエステルフィルムとした複合ウェブの引張ヤング率の計算結果を紹介する。

PETフィルムとポリエステルフィルムの引張ヤング率を一定とみなした場合の計算例である。PETフィルムのヤング率と厚みをE1=4860[MPa](=4860×106[Pa])とt1=49.8[μm] (=49.8×10-6[m])、ポリエステルフィルムのヤング率と厚みをE2=230[MPa] (=230×106[Pa])とt2=69.5[μm] (=69.5×10-6[m])とした。これまでに説明してきた結果を参考にしている。
それぞれの値を式(10)に代入して解くと、複合ウェブの引張ヤング率は2160[MPa]と算出できる。
これは各層のヤング率を一定とみなした場合である。次に近似式で表現したヤング率をもちいた場合の例を示す。

引張ヤング率をPETフィルムで一定、ポリエステルフィルムで近似式とした場合の計算例である。ここで、ポリエステルフィルムの近似式E2は次のように表現でき、これ以外のE1とt1とt2は前述と同じ値とした。
![]()
式(12)を式(10)に代入すると、次式が得られる。
![]()
結果として、近似式をもちいた場合の複合ウェブの引張ヤング率は、近似式を含んだ形で表現される。具体的な数値にする場合は、式(12)に所定の張力Tを代入してE2を算出し、これを式(13)に適用すればよい。
例えば張力がT=200N/mであれば、式(12)から
![]()
となる。この結果を式(13)に代入して解くと
![]()
となり、近似式をもちいた場合の複合ウェブの引張ヤング率が算出される。これは、ある一点の張力に対するヤング率の値である。一方、任意の張力に対応する1つの近似式で表現することもできる。式(12)と式(13)から任意の張力に対する引張ヤング率Eを計算し、これを近似した式をもちいればよい。

グラフには、既に数値化・数式化したPETフィルムとポリエステルフィルムの引張ヤング率に加え、各ウェブを貼り合わせた複合ウェブの引張ヤング率の計算値を示している。描画範囲は50~350N/mであり、ポリエステルフィルムの近似範囲にあわせている。
複合ウェブの引張ヤング率の計算値を近似すると、次式が得られる。
![]()
任意の張力Tにおける複合ウェブの引張ヤング率Eを算出できるため、理論計算には上式を適用すればよい。なお、近似範囲外への対応は、上述した「近似値の落とし穴と対処例」を参考にしてほしい。
巻取解析ソフトでの設定と計算結果例
巻取解析ソフトにおける引張ヤング率(円周方向ヤング率)の設定方法、および計算結果の例を示す。
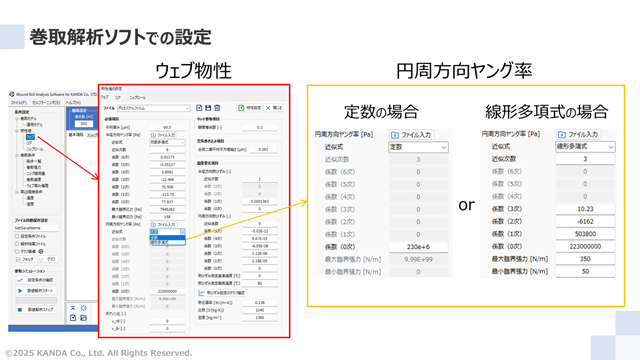
巻取解析ソフトのメイン画面における条件設定の「ウェブ」をダブルクリックすると、ウェブ物性の設定画面が表示される。この画面の必須項目の円周方向ヤング率における近似式のドロップダウンリストから「定数」あるいは「対数多項式」を選択して数値を入力する。
ここでは、上述したポリエステルフィルムを例に説明する。なお、引張ヤング率は一定とする場合では230[MPa] (=230×106[Pa])、近似式とする場合では3次の線形多項式近似した次式であった。
![]()
定数を選択する場合
引張ヤング率を一定とする場合に選択する。円周方向ヤング率の設定では、係数0に230e+6と入力する。なお、"e+6"は対数表示の106を意味している。230000000と入力することと同じである。
線形多項式を選択する場合
引張ヤング率を近似式とする場合に選択する。なお、近似式は線形多項式での近似を前提にしている。円周方向ヤング率の設定では、近似次数に3を入力し、各次数に対応した係数をそれぞれ入力する。ここでは、対数表示であった式(17)の係数を実数表示で入力している。対数表示のまま入力しても問題ない。また、「近似値の落とし穴と対処例」で紹介した近似範囲50~350N/mに対応させるため、臨界最小張力に50、臨界最大張力に350と入力する。
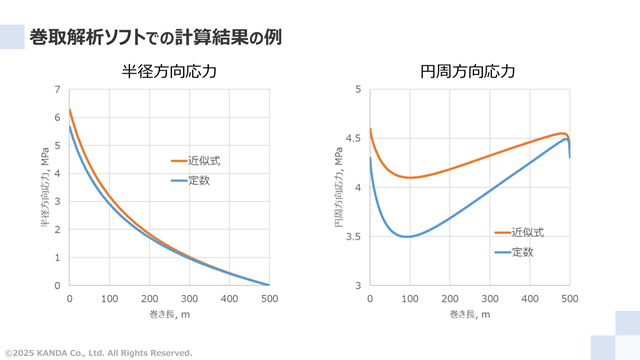
円周方向ヤング率を一定とした場合と近似式とした場合の計算結果の例を示している。左図は半径方向応力、右図は円周方向応力の結果である。適用モデルはシンプルにHakielモデルとし、各種オプション(巻き込み空気の影響や温度変動の影響、ウェブ厚みムラの影響)は未考慮とした。また、巻取り条件は張力を300N/m、巻き長を500mとしている。
円周方向ヤング率の設定が異なると、半径方向応力と円周方向応力のいずれにも差があった。この差が大きいか小さいかの判断は状況によって異なる。しかし、どちらが適切かといえば、より現実的な張力の依存性を考慮した近似式の方であろう。
円周方向ヤング率の受託評価サービスを行っている。希望される場合は「お問い合わせ」から相談いただきたい。
関連ページ
 ウェブハンドリング
ウェブハンドリング