巻取ロール内のウェブには半径方向応力が作用し、ウェブの厚み方向に力が負荷された状態になる。この力によってウェブは変形して薄くなる。ウェブが力によって変形した際に、元に戻ろうとする強さ(弾性)を圧縮ヤング率という指標で評価する。ここでは、ウェブ厚み方向の圧縮ヤング率を算出するプロセスを具体的に紹介する。なお、巻取理論における半径方向ヤング率とは、この圧縮ヤング率のことを指している。
材料力学の基礎「応力とひずみとヤング率」について
圧縮ヤング率を評価するベースである材料力学について、その基礎である「応力」と「ひずみ」と「ヤング率」を説明する。
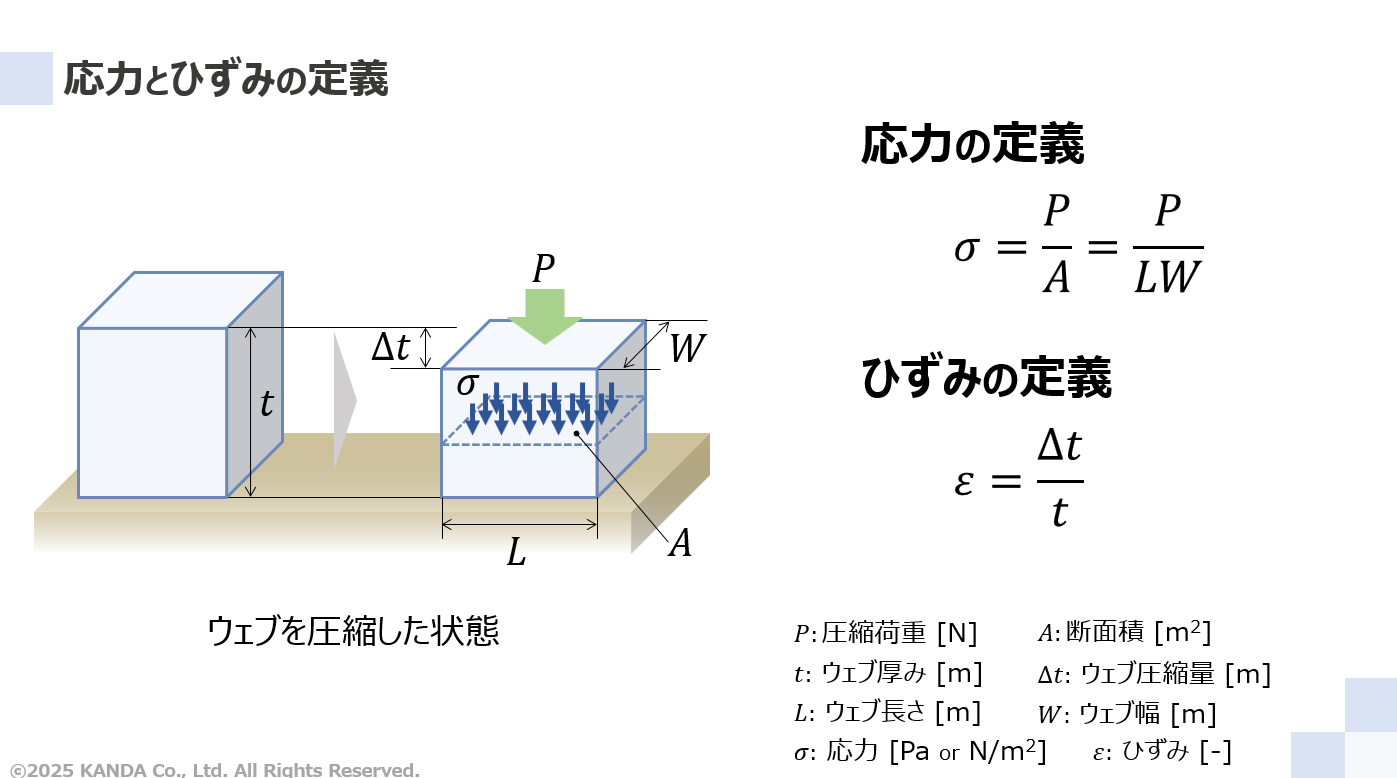
厚みt[m]のウェブに圧縮荷重P[N]が作用し、鉛直方向に縮み量Δt[m]だけ変形した状態を図に示している。なお、ウェブの長さをL[m]、幅をW[m] 、断面積をA[m2]で表している。外力が作用して変形する固体の挙動を取り扱う材料力学では、“外力と変形”を寸法によらないように一般化した”応力とひずみ”で表現する。ここで、材料力学では引張を正、圧縮を負とし、符号で力や変形の方向を表すのが一般的である。しかし、この技術情報では"圧縮を正"として取り扱う。
ウェブを圧縮荷重Pで圧縮したときに、その断面Aに一様な力が分布すると考える。この一様な力を合わせるとPに等しい。このとき、単位面積当たりの力を応力σと呼び、次式で与えられる。
![]()
ここで、応力の単位は式(1)から[N/m2]であるが、パスカル[Pa]でも表される。
一方、材料に圧縮荷重Pが加わると変形して縮む。このときの縮み量Δtを元の厚みtで割った値をひずみεと呼び、次のように定義される。
![]()
ここで、ひずみの単位は式(2)から[m/m]であり、無次元量[-]で表される。ひずみは元のサイズに対する縮み量の割合を意味している。
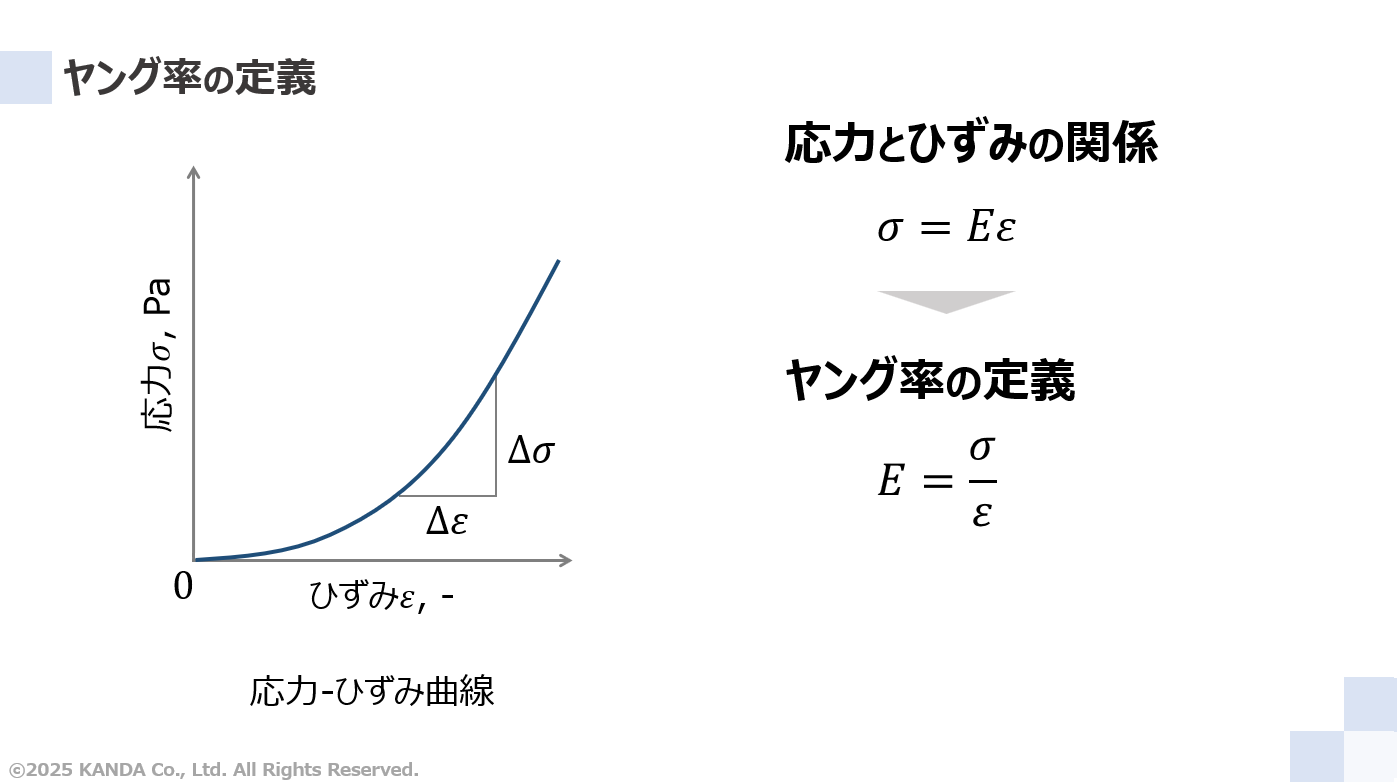
圧縮試験で計測した荷重と縮み量を式(1)と式(2)にそれぞれ代入すると、応力とひずみの値が計算できる。これらのデータをグラフ化すると、図のように応力‐ひずみ曲線を描くことができる。このとき、応力とひずみの関係に比例定数(傾き)Eをもちいると、次のように表される。
![]()
比例定数Eは材料固有の値である。いくつかの名称があるが、ここではヤング率という名称を使う。式(3)より、ヤング率は次式で与えられる。なお、単位は[Pa]が一般的である。
![]()
圧縮試験とその実例データ
圧縮試験の方法について説明し、あるプラスチックフィルムをもちいた試験データの実例を示す。
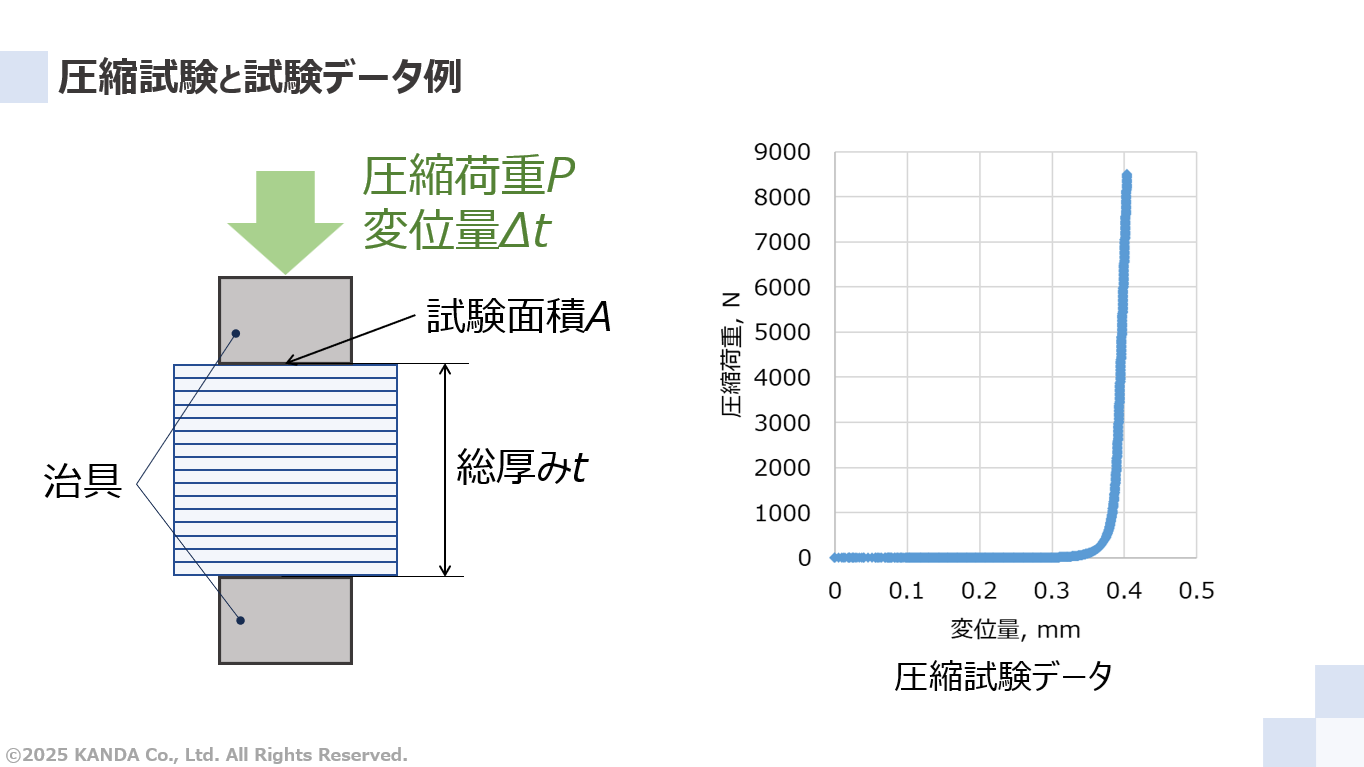
圧縮試験に用いられる万能材料試験機には、サンプルを挟み込む二つの治具と、その片方に力を計測するロードセルが取り付けられている。ここでサンプルと治具の接触する面積が試験面積A[m2]となる。
試験準備として、治具よりも大きくカットして積層したサンプルを作成する。このとき積層数N[枚]をカウントするとともに総厚みt[m]を測定しておく。次に積層サンプルを下側の治具に置いた後、上側の治具を降下させていき、サンプルと接触する直前で止める。ここで、試験サンプルのサイズを治具よりも大きくする理由は、サンプルカット時のバリの影響を抑えること、試験面積をサンプルではなく治具の面積で設定することにある。
圧縮試験中は、治具の変位量Δt[m]と圧縮荷重P[N]のデータを随時取得する。
ある二軸延伸ポリエチレンテレフタレートフィルムを用いて圧縮試験をおこなった。取得した変位量と圧縮荷重のデータをもとに作成したグラフに示している。ここで、この結果はこのフィルム固有のものであり、すべてのポリエチレンテレフタレート(PET)フィルムを代表するものではない。プラスチックフィルムの圧縮ヤング率は原材料や表面粗さなどの影響を受ける。その他の分類のウェブ※であっても同様のことがいえる。特に紙や織布・不織布では、その内部構造や密度の影響を受ける。
※紙、金属箔、織布・不織布、異種材料を貼合したウェブや表面塗工したウェブといった複合ウェブなど
試験条件として試験面積を707mm2、変位速度を5μm/sec、データ取得時間を0.2sec/データとし、終了判断※を圧縮応力が12MPaに達した時点としている。終了判断について、巻取ロール内の半径方向応力は数MPa程度になることがあり、過大に設定している。なお、サンプルの積層数は105枚、実測した総厚みは5.23mm、取得したデータ点数は結果的に800程度であった。
※終了判断は"ロードセルを故障させない"ために最大容量の90%以下になるようにしている。わずかな変位量でも圧縮荷重が極端に高くなって最大容量を超えてしまう危険性を回避するためである。パーセンテージが低いほど安全である。
サンプルの圧縮状態の確認
巻取ロール内のウェブには半径方向応力が作用しており、このときのウェブ同士は面で接触している。そこでウェブの圧縮ヤング率を適切に評価するために、サンプルに負荷される荷重が均一であるかを確認する。

左の写真は試験サンプル近傍の測定部であり、サンプルを特別に制作した圧縮治具※で挟んだ状態を示している。右の写真は圧力によって発色濃度が変化する感圧フィルムを用い、圧縮治具とサンプルの接触状態を可視化したものである。ここで、標準治具とは試験機に付属する標準の治具、特別治具とはウェブ厚み方向の圧縮試験用に特別に制作した治具である。また、特別治具に接触式変位計を設けている理由は、次の「試験データの信頼性の確認」で紹介する。
※試験機メーカーの標準治具ではない。ウェブの厚み方向の圧縮試験に特化した独自設計治具
圧縮状態の可視化結果から、標準治具の場合は圧縮荷重が主に治具の外周部に集中して作用していることがわかる。つまり、治具表面が凹状になっており、サンプルはこの状態で圧縮される。これではサンプルには均一な荷重が負荷されない。標準治具の課題解決のため、特別治具では治具表面を平坦にし、より均一な荷重が負荷されるようにしている。
ウェブ厚み方向の圧縮ヤング率を適切に評価するには、巻取ロール内の状態と同じように、サンプルへの負荷荷重をより均一にする工夫が必要であろう。
試験データの信頼性の確認
圧縮試験では荷重と変位量のデータを取得し、これらのデータを処理していって圧縮ヤング率を数値化する。したがって、それぞれのデータの信頼性を確認しておかないと、算出した圧縮ヤング率の信頼性は疑われる。
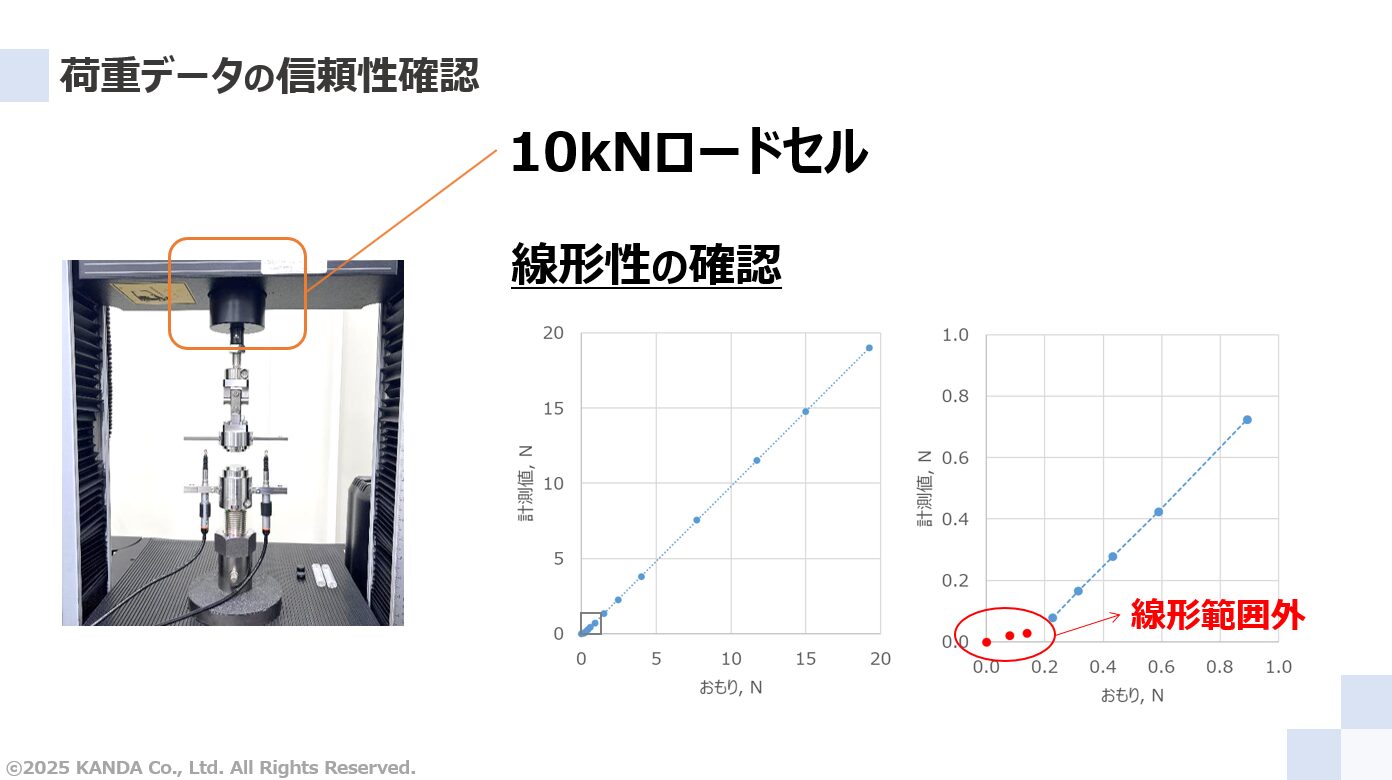
圧縮ヤング率の評価に必要な計測データは荷重と変位のデータである。はじめに荷重データの信頼性について考える。
圧縮ヤング率は巻取りの理論モデルへの適用を想定している。そのため、巻取ロール内での想定される半径方向応力の範囲が圧縮試験での応力範囲になる。
最大容量10kNのロードセルを用いたのは、最大で圧縮応力10MPa以上のデータを取得することを考えてのことである。一方、最低の圧縮応力は1kPa程度が必要である。圧縮試験の応力範囲を1kPa~10MPaとしたとき、試験面積を考慮すると圧縮荷重の範囲はおおむね1~10000Nになる。計測したい最低荷重1Nはロードセル最大容量10kNの0.01%にあたり、ロードセルの精度補償外であることが多い。
図中のロードセルを試験機から外して逆さにし、重量がわかっているおもりを置いたときの荷重データを計測した。グラフはおもり重量に対する荷重データであり、左図は0~20Nの範囲、右図は0~1Nの範囲の結果をそれぞれ示している。左図では線形性があるように見えるが、右図では0.2N以下でそうはなっていない。
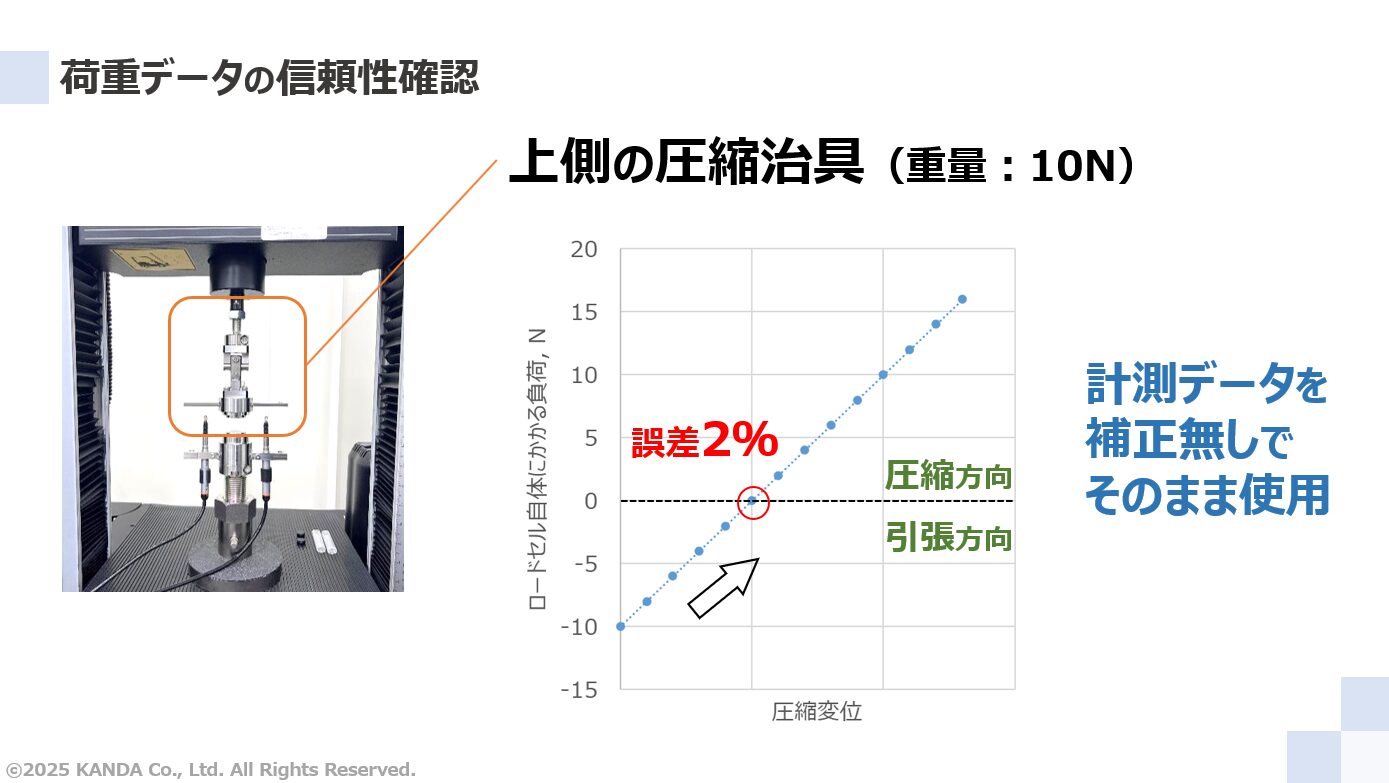
圧縮試験を開始するときは、写真のように圧縮治具を取り付けた状態にし、変位と荷重は万能材料試験機のソフトウェアでゼロ点調整される。このとき、ロードセルには上側の圧縮治具の重量10Nが引張方向(自重方向)に負荷されている。
グラフは圧縮変位の増大にともなって変化する、ロードセル自体にかかる負荷を表している。ゼロ点調整後のソフトウェアで表示される荷重ではない。ロードセル自体にかかる負荷の方向は、試験開始時点では引張方向であるが、上側圧縮治具の重量10Nを超えたところで圧縮方向(自重方向とは逆方向)に変わる。この変化点の0.2Nの範囲で上述した線形範囲外のデータが含まれることになる。取得する荷重データ10Nに対して0.2Nであり、計測誤差は2%になる。この程度であれば許容できるとし、計測データを補正なしでそのまま使用することにする。
次に変位データの信頼性について確認する。 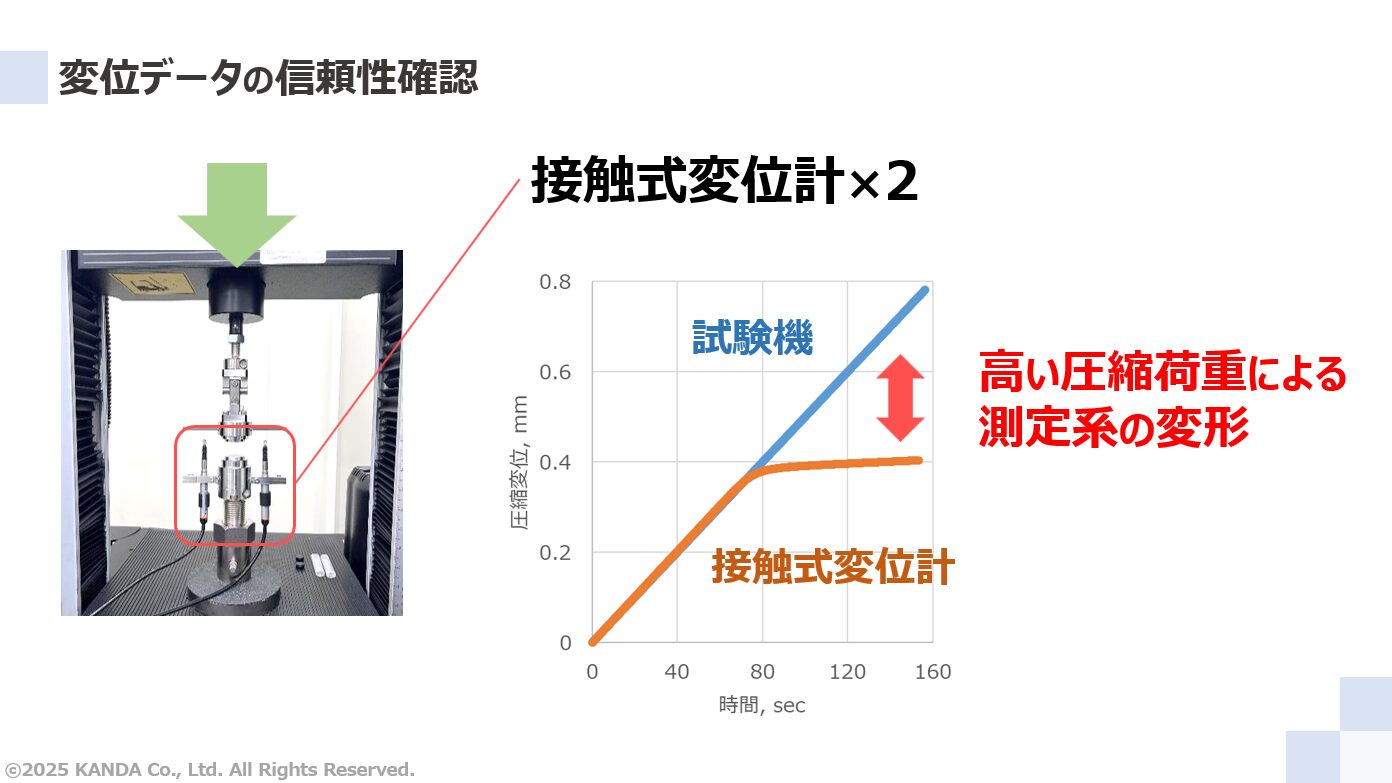
図中のグラフは圧縮試験で取得した試験機および接触式変位計の変位データの時間変化を示している。試験機の変位データは線形に増大していく。一方、接触式変位計の変位データは試験初期こそ線形に増大していくが、途中から変位の増大量は低下していった。
接触式変位計はサンプルを挟む測定部の直近の圧縮治具に取り付けている。したがって、接触式変位計の変位データは試験機のそれよりもサンプルの圧縮変形を適切に表していると言えよう。一方、試験機は一定速度で押し込んでいるつもりが、高くなっていく圧縮荷重による測定系の変形(治具の固定ピンなど)により、実際には設定どおりにサンプルを押し込めていないと考えられる。
圧縮ヤング率を算出するための変位データとしては接触式変位計の方が適切である。接触式変位計を設置できない場合は、いわゆる空打ちしたデータをもとに圧縮試験のデータを補正処理する方法がある。なお、この空打ちではロードセルを故障させないように細心の注意が必要になる。金属同士の圧縮試験になるため、極めてわずかな変位でもロードセルの最大容量を簡単に超える場合がある。
試験データから応力とひずみを計算
圧縮試験で取得した荷重データと変位データから、応力とひずみの値をそれぞれ計算する。
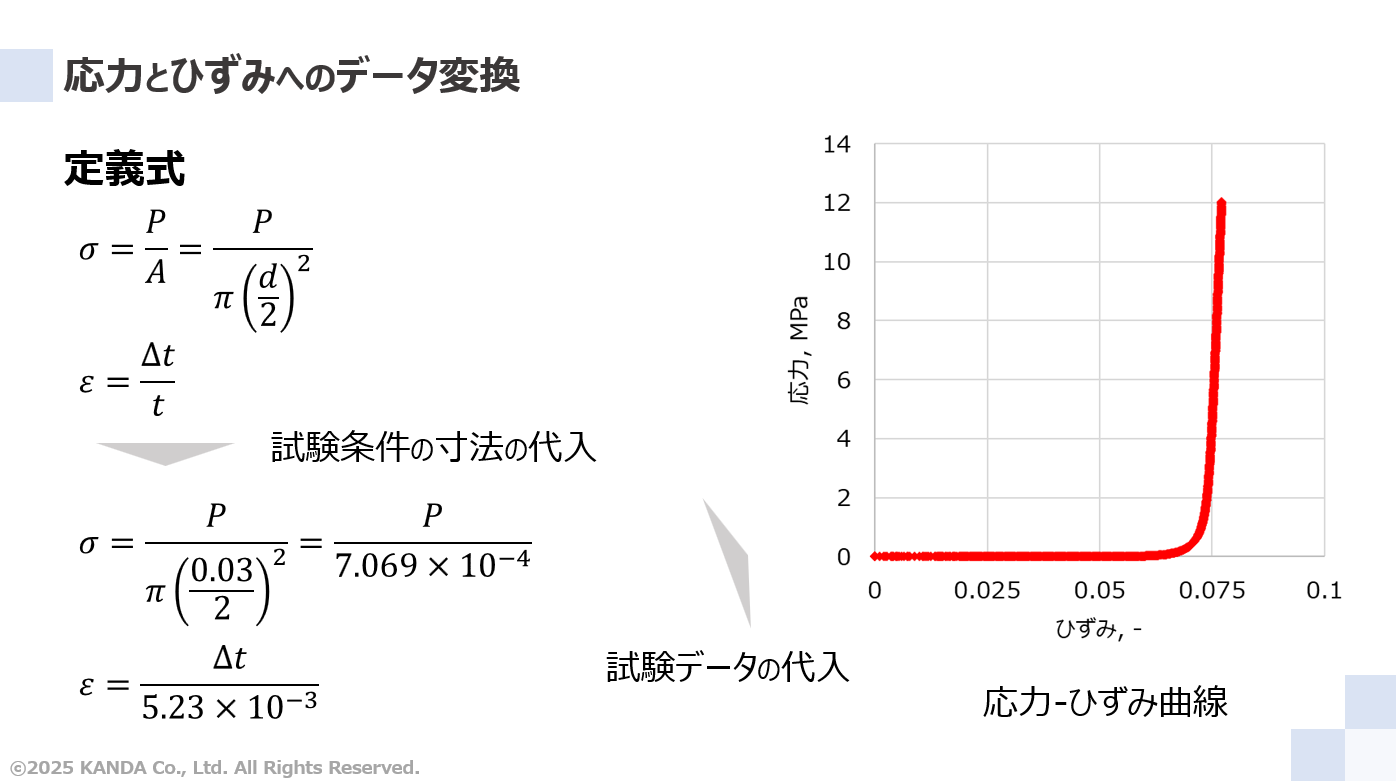
式(1)の応力σの定義式および式(2)のひずみεの定義式の試験サンプルの寸法を代入すると、それぞれ次のように表される。なお、代入する数値は[m]に換算し、試験面積は圧縮治具の直径d=30mm=0.03mからA=7.069×10-4m2、試験サンプルの厚みt=5.23mm=5.23×10-3mとしている。
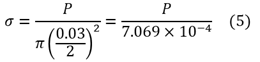
![]()
これらの式に圧縮試験で取得したデータの圧縮荷重Pと圧縮変位Δtを代入すれば、応力σとひずみεの値がそれぞれ算出される。この結果から作成した応力-ひずみ曲線のグラフを図に示している。
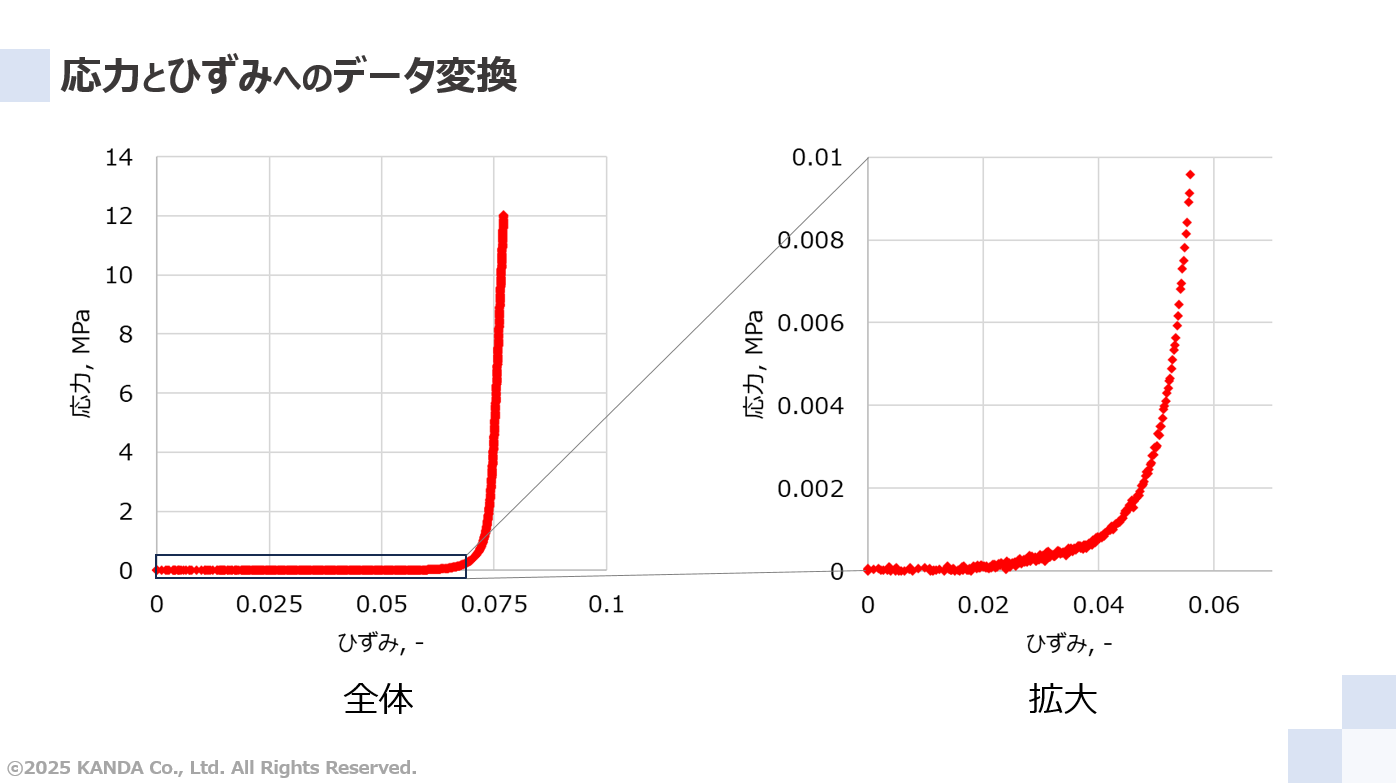
左図のように応力-ひずみ曲線を圧縮試験範囲の全体でみると、ひずみが0.07付近まで応力は0のように見える。しかし、この範囲を拡大してみると、圧縮ひずみの増大にともない圧縮荷重も増大していることが確認できる。
応力-ひずみ曲線の非線形性について
ウェブの圧縮試験における応力-ひずみ曲線は試験初期から非線形性を示す。これはウェブの潰れ方に起因する。
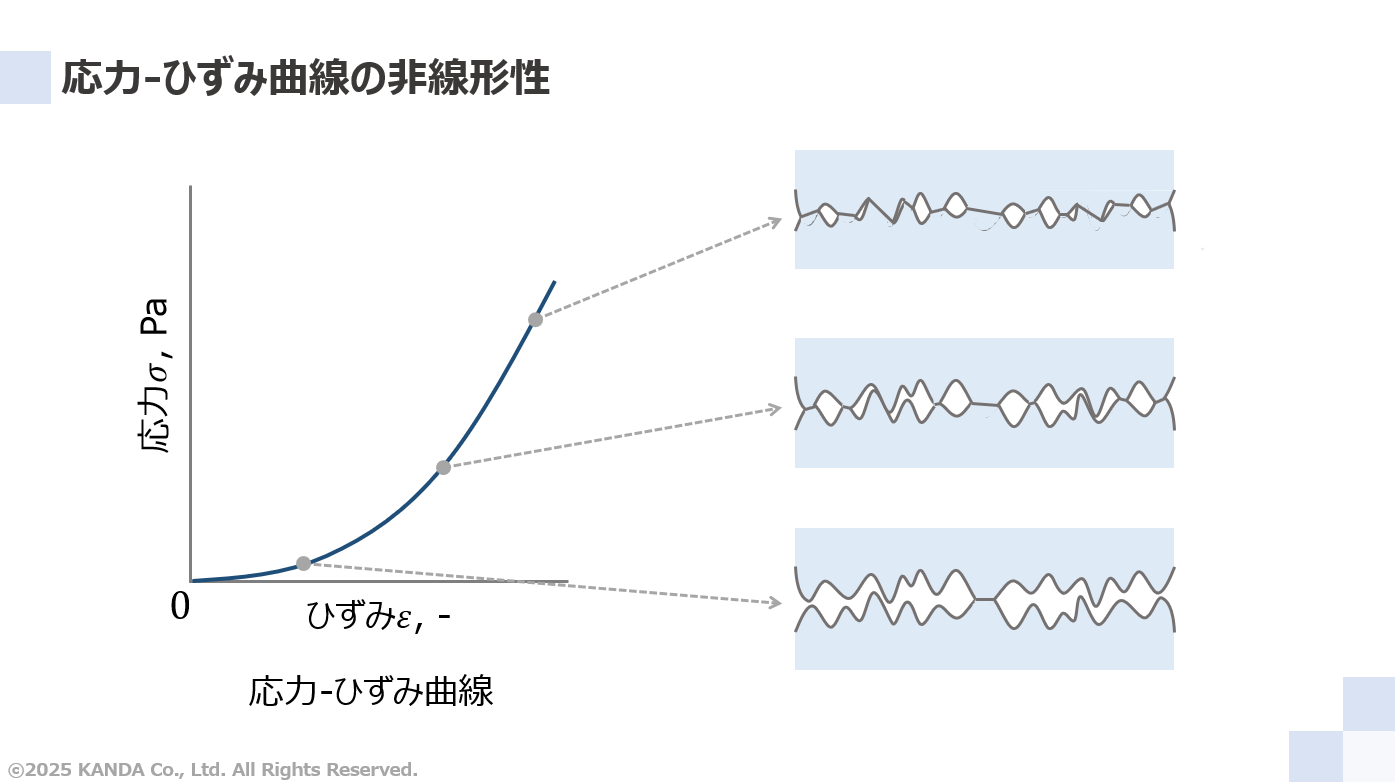
プラスチックフィルムの場合、その表面と裏面には大小無数の粗さ突起が存在する。図中には応力-ひずみ曲線とその値に対応する粗さ突起の潰れ具合のイメージを示している。
圧縮試験の初期は粗さ突起が潰れの影響が支配的であり、徐々にバルクの影響が大きくなっていくと考えられる。したがって、この粗さ突起が応力-ひずみ曲線の非線形性に起因しているといえる。ウェブ自体に空隙のない、金属箔や表面塗工したプラスチックフィルムも同様に考えられる。空隙のある紙や織布・不織布の場合は、その内部構造や密度にも起因するだろう。いずれにしても、ほぼ全てのウェブにおいて圧縮試験の応力-ひずみ曲線は非線形性を示し、これにはウェブの潰れ方が関係する。
したがって、同じ素材のウェブであっても対象のウェブごとに圧縮試験をし、それぞれの圧縮ヤング率を算出することが好ましい。
圧縮ヤング率の算出方法
巻取りの理論計算では、応力の関数で表した圧縮ヤング率を与える。したがって、圧縮試験の結果をもとに任意の応力における応力-ひずみ曲線の傾きを求めていき、この近似式を圧縮ヤング率として定義する。
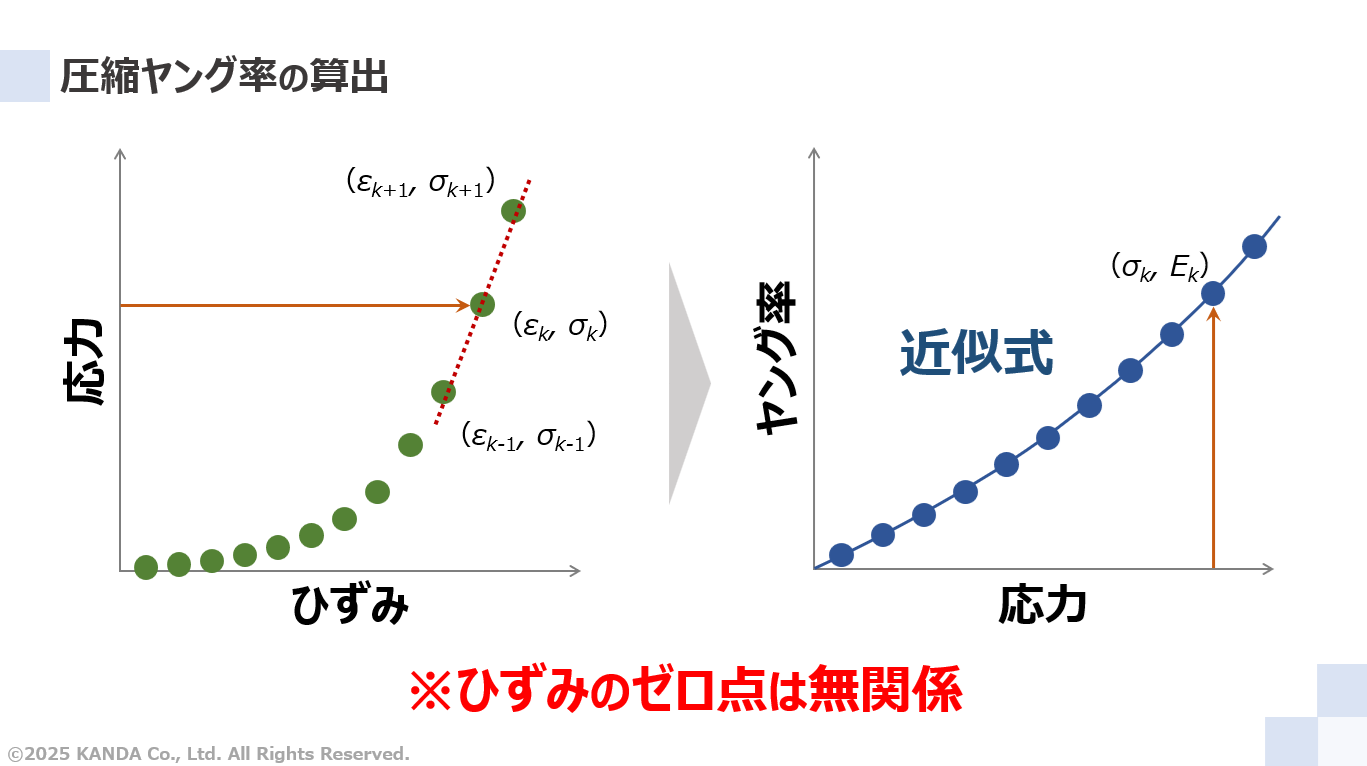
左図は応力-ひずみ曲線のデータをプロットしたイメージであり、データNo.kにおける応力とひずみの値を(εk, σk)、およびその前後の値を(εk-1, σk-1)と(εk+1, σk+1)で示している。このとき、応力σkでの圧縮ヤング率Ekは次式の中央差分で求められる。
![]()
この結果として右図の応力とヤング率のグラフに(σk, Ek)をプロットできる。他のデータに対しても同様に計算する。その後、応力とヤング率の関係を近似すれば、その近似式が応力を関数とした圧縮ヤング率になる。
圧縮ヤング率は式(7)で示しているように応力差とひずみ差から計算している。したがって、応力差に対しては荷重データの線形性が重要であり、絶対値は試験機のソフトウェア上でゼロ点調整できるので特に問題にはならない。また、ひずみについてはひずみ差が重要であってゼロ点は重要ではない。
応力とヤング率のグラフ
「試験データから応力とひずみを計算」で作成した応力-ひずみ曲線をもとに、応力とヤング率の関係をグラフ化する。
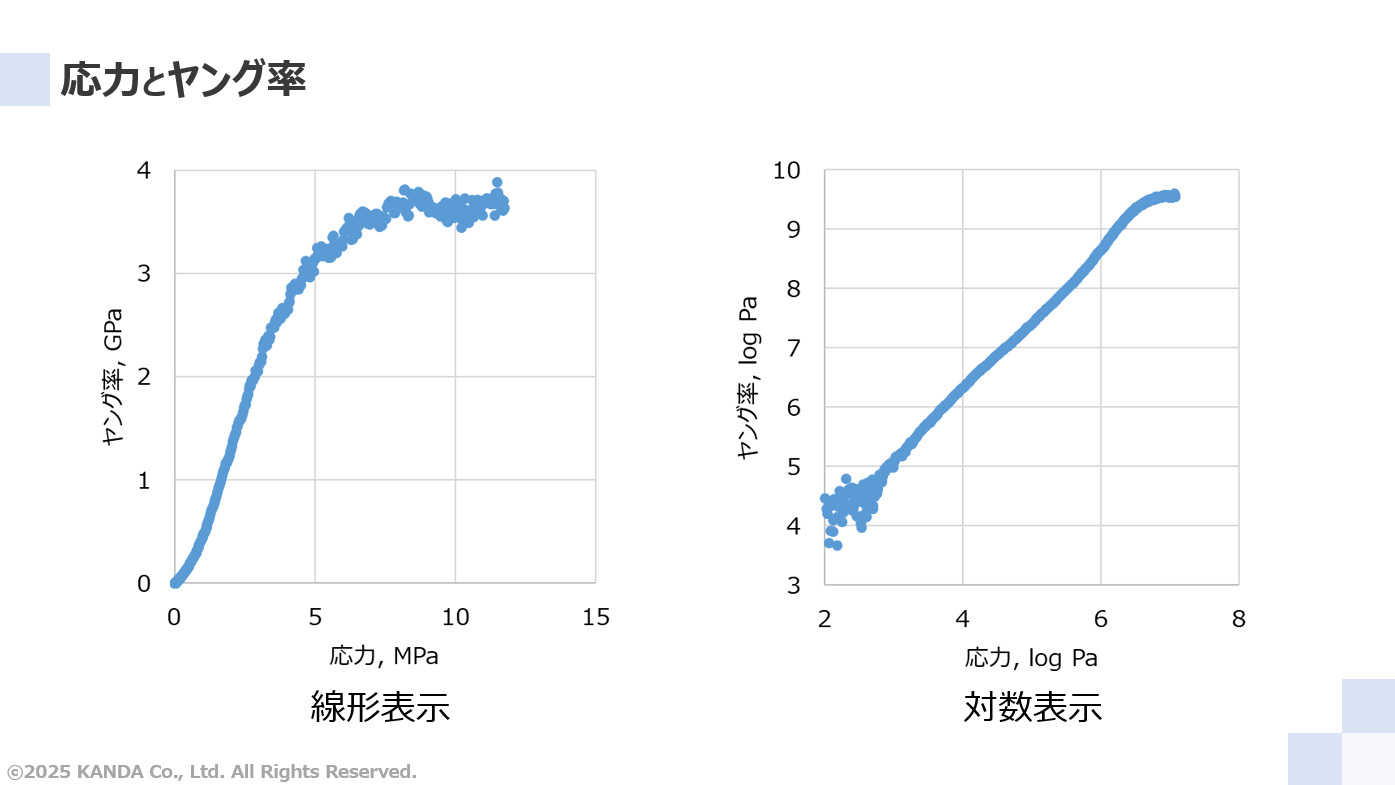
前述した「圧縮ヤング率の算出方法」の方法でグラフ化した2つの結果を図に示している。それぞれのグラフは軸が異なり、左図は線形、右図は対数で表示している。線形表示は応力の高い側、対数表示は応力の低い側における近似精度を確認するためである。ここで、応力とひずみのデータを平均化処理した値をもとにグラフ化している。応力はノイズの影響、ひずみは変位分解能の影響を抑えるためである。
2つのグラフから、ヤング率は応力とともに増大していき、応力7MPa(=6.8 log Pa)以上でおおむね一定となった。このような傾向になる要因は「応力-ひずみ曲線の非線形性について」で記述したとおりである。
応力とヤング率のグラフを近似した近似式を圧縮ヤング率として取り扱うが、これにはいくつかの近似式が提案されている。
近似式の選択とその近似精度
巻取りの理論モデルに適用する圧縮ヤング率の近似式は、大別して3つの種類が提案されている。これらの近似式をこれまでに示した測定データに適用し、それぞれの近似精度を確認する。

巻取りの理論モデルに適用する圧縮ヤング率の近似式は大別して線形多項式近似、累乗近似、対数多項式近似の3つの種類が提案されている。具体的な近似式およびその例、参考論文などを下記する。結論を言えば、対数多項式が最もフィッティングしやすく近似精度が高いといえる。
線形多項式近似
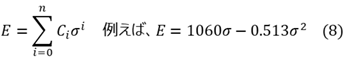
- Z. Hakiel, “Nonlinear Model for Wound Roll Stress,” TAPPI Journal, Vol. 70, No. 5, (1987), pp. 113-117.
- W.R. Qualls and J.K. Good, “Thermal Analysis of a Round Roll,” ASME Journal of Applied Mechanics, Vol. 64, No. 4, December, 1997, pp. 871-876.
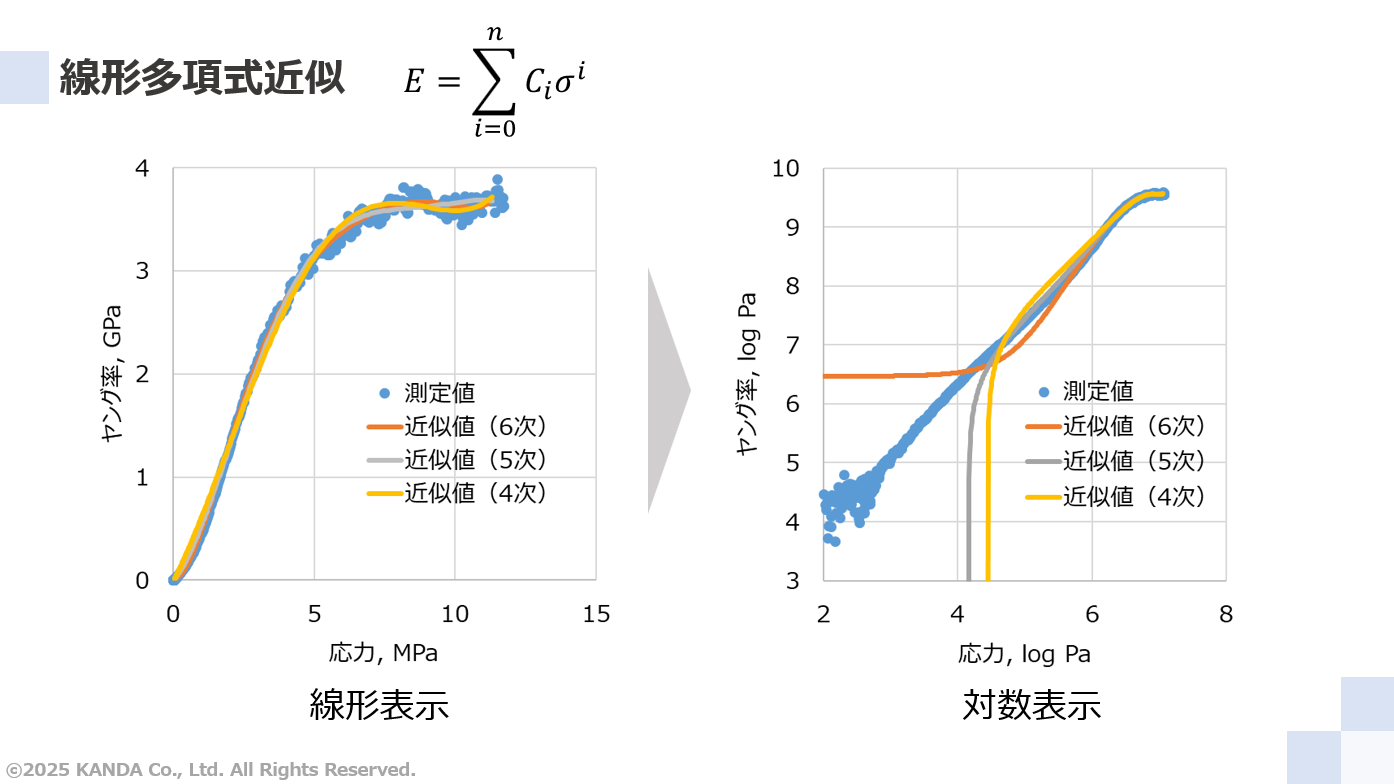
累乗近似
![]()
- 谷本光史, 河野和清, 他, “空気巻き込みを考慮した巻取りロールの内部応力解析,” 日本機械学会論文集A編,Vol. 68, No. 665, (2002), pp. 161-168.
- 神田敏満, 朱峰承興, 橋本巨, “端部からの空気流出を考慮した巻取りロールの内部応力解析,” 日本機械学会論文集C編,Vol. 76, No. 772, (2010), pp. 3736-3743.
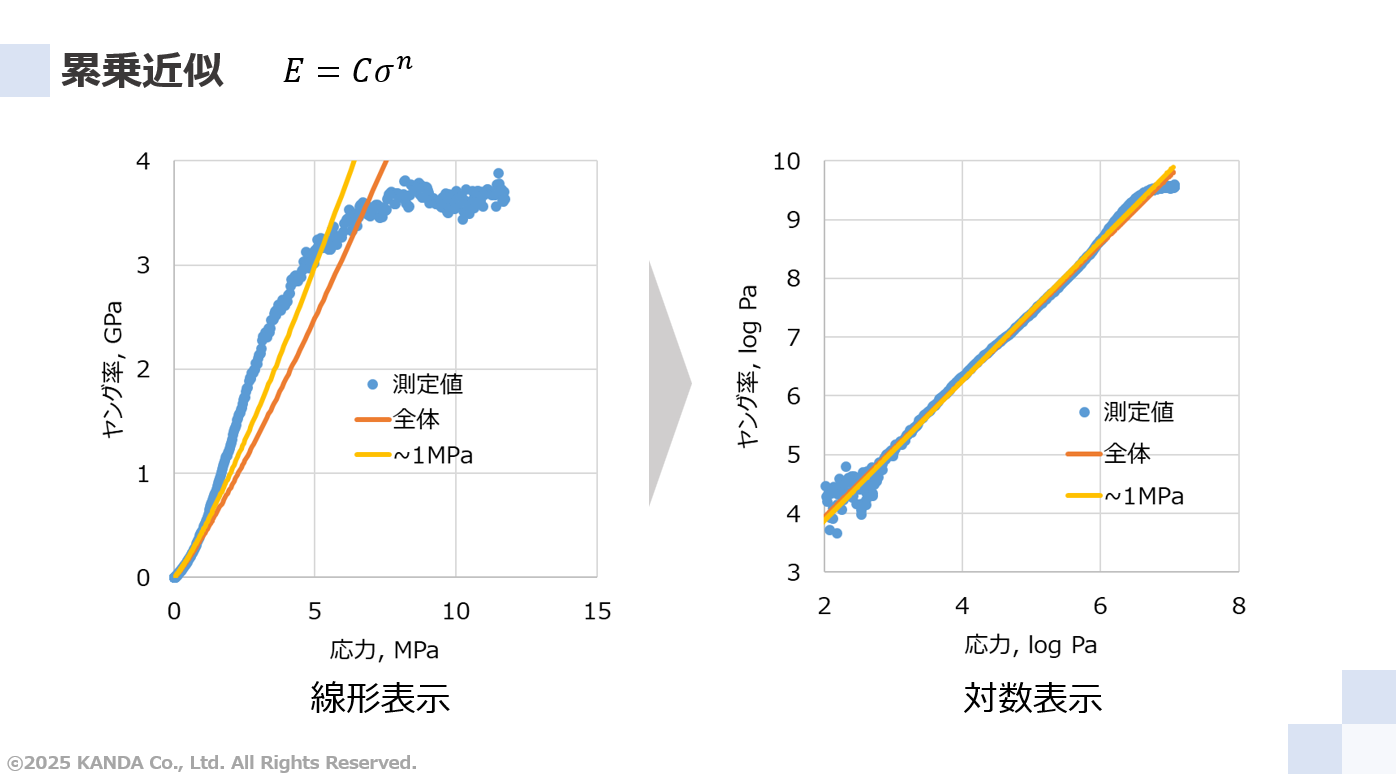
対数多項式近似
![]()
- 巻取解析ソフト(詳細は「巻取解析ソフトでの設定と計算結果例」で紹介)
次に、これまでに紹介した応力とヤング率の関係の実際のデータを用い、各近似式でフィッティングしたときの特徴やその近似精度を確認する。なお、線形多項式近似と対数多項式近似でフィッティングするときの近似次数は、エクセルで設定可能な範囲にしている。
左図の線形表示の測定値を用いて多項式近似した近似値をそれぞれのグラフに示している。この近似を線形多項式近似と呼ぶことにする。なお、近似次数を4次、5次、6次としたときの近似値をそれぞれ示している。左図の線形表示のグラフでは、いずれの近似次数でもよくフィッティングしているように見える。
一方、右図の対数表示のグラフで見ると、おおむね6 log Pa(線形表示では1MPa)以下の近似精度はいずれもよくない。特に近似次数が4次と5次の場合において、圧縮ヤング率は4~4.5 log Pa以下で極端に低下し、グラフ描画範囲外であるがマイナスの値になった。
ここで、ウェブが力によって変形した際に元に戻ろうとする強さ(弾性)を圧縮ヤング率で表している。本技術情報の定義した圧縮ヤング率の符号の場合はプラスである。この符号がマイナスであることは、ウェブを押し込んだ時に元に戻ろうとせずに縮もうとする変形になるということを意味している。
したがって、理論モデルに適用する近似式として近似次数が4次と5次のものは不適切であり、採用できるのは式(11)で表される6次の近似式のみである。しかしながら、応力が6 log Pa(1MPa)以下の近似精度は十分とは言えない。
![]()
線形多項式近似の特徴として、線形表示(応力が高い側)では近似精度が良いように見えるが、対数表示(応力が低い側)ではそうではないことがある。加えて近似値がマイナスになる範囲があるかどうかの確認も必要である。
ここで、式(11)の近似係数の桁数は過剰のように感じるかもしれない。しかしながら、これは桁数が近似値に及ぼす影響を考慮した結果である。具体的な影響については次の論文のp4235に記載している。
- 神田敏満, 橋本巨, “プラスチックフィルムの粘弾性特性を考慮した巻取りロール内部の熱応力解析 (第1 報,ポリプロピレンフィルムにおけるクリープコンプライアンスの応力・温度依存性),” 日本機械学会論文集C編, Vol. 77, No. 783, (2011), pp. 4228-4238.
線形多項式近似の場合と同様に、左図の線形表示の測定値を用いて累乗近似した近似値をそれぞれのグラフに示している。右図はこの結果を対数表示にしたものである。なお、各グラフ中には近似した測定値の範囲が異なる近似値を示している。"全体"と"~1MPa"の2つの範囲である。
左図の線形表示のグラフを見ると、おおむね1MPa以上の近似精度はいずれも良くない。一方、右図の対数表示のグラフで見るとよくフィットしているように見える。
理論モデルに適用する近似式は、式(12)で表される近似範囲を低応力側とした~1MPaの方がより適切である。理論モデルでは巻取張力起因の低応力側からスタートし、巻取りの進行にともなって徐々に応力が高くなっていく計算になる。つまり、低応力側のヤング率の近似精度が重視される。この考え方は累乗近似のみならず他の近似方法においても同じである。
![]()
累乗近似の特徴として、線形表示(応力が高い側)ではそうではないが、対数表示(応力が低い側)では近似精度が良いといえる。
線形多項式近似や累乗近似とは異なり、右図の対数表示の測定値を用いて多項式近似した近似値をそれぞれのグラフに示している。この近似を対数多項式近似と呼ぶことにする。
圧縮ヤング率の測定値と式(13)の近似式による近似値は左図の線形表示のグラフと右図の対数表示のグラフのいずれにおいてもよくフィットし、線形多項式近似や累乗近似と比べて近似精度が高いことがわかる。
![]()
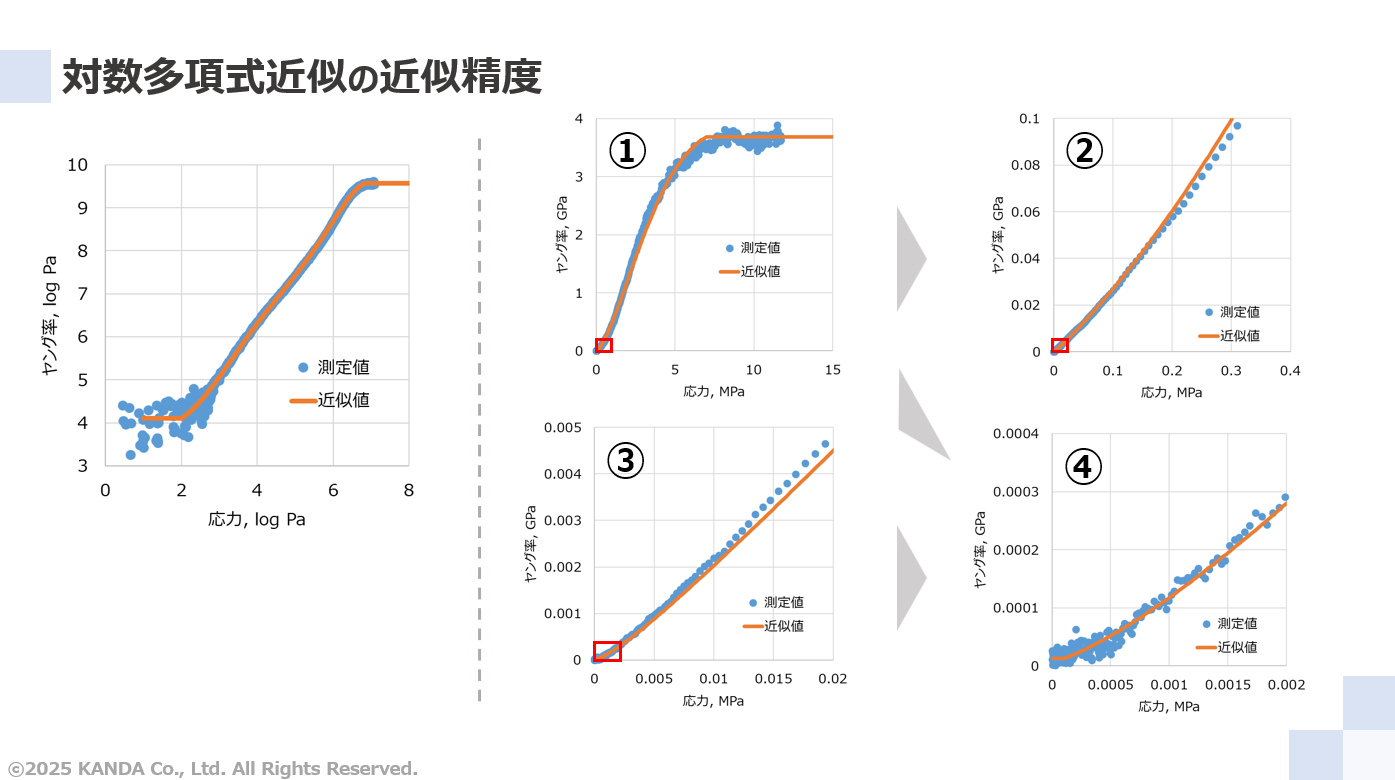
後述する近似値に関する問題に対処した結果をもとに、近似精度についてより詳しく確認する。図中の破線から左側が対数表示のグラフ、右側が線形表示のグラフであり、いずれも測定値と近似値を示している。
対数表示ではよく一致している。次に、線形表示での近似精度を確認する。図中のグラフに表示している①~④の番号および赤枠は、番号が大きくなるほど赤枠の領域を拡大したグラフであることを意味している。①は測定範囲全体でありよく一致している。②~④と徐々に拡大していってもよく一致していることが確認できる。
これらの結果より、対数多項式近似は低応力から高応力までの広い範囲で近似精度の高い近似方法といえる。
各種ウェブの圧縮ヤング率
PETフィルム以外のウェブの圧縮ヤング率を紹介する。
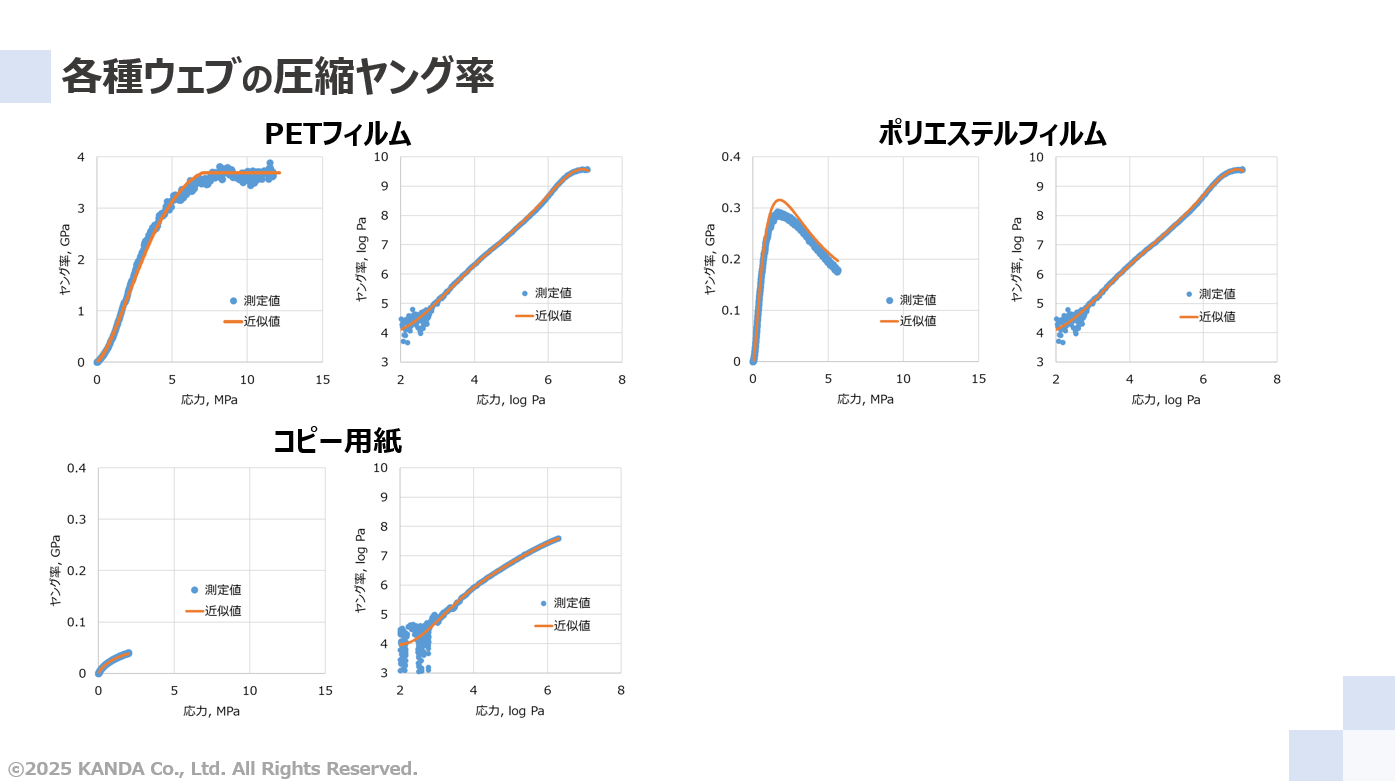
PETフィルムに加え、ポリエステルフィルム、コピー用紙の応力と圧縮ヤング率の関係について、測定値と対数多項式近似での近似値の結果を線形表示と対数表示のグラフでそれぞれ示している。なお、各ウェブはある特定のウェブであり、同じ分類や製品を代表するものではない。
ここで、対数表示のグラフの応力とヤング率の範囲は同じである。一方、線形表示のグラフの場合、応力の範囲は同じであるものの、ヤング率の範囲はPETフィルムに比べてそれ以外のウェブで1桁小さいことに注意してほしい。
これらの結果から圧縮ヤング率は各ウェブで異なり、PETフィルムに比べてポリエステルフィルム、コピー用紙の順に小さいことがわかる。
近似値の落とし穴と対処例
近似範囲外の近似値は予期しない値になる場合がある。したがってその対処をしておく必要がある。
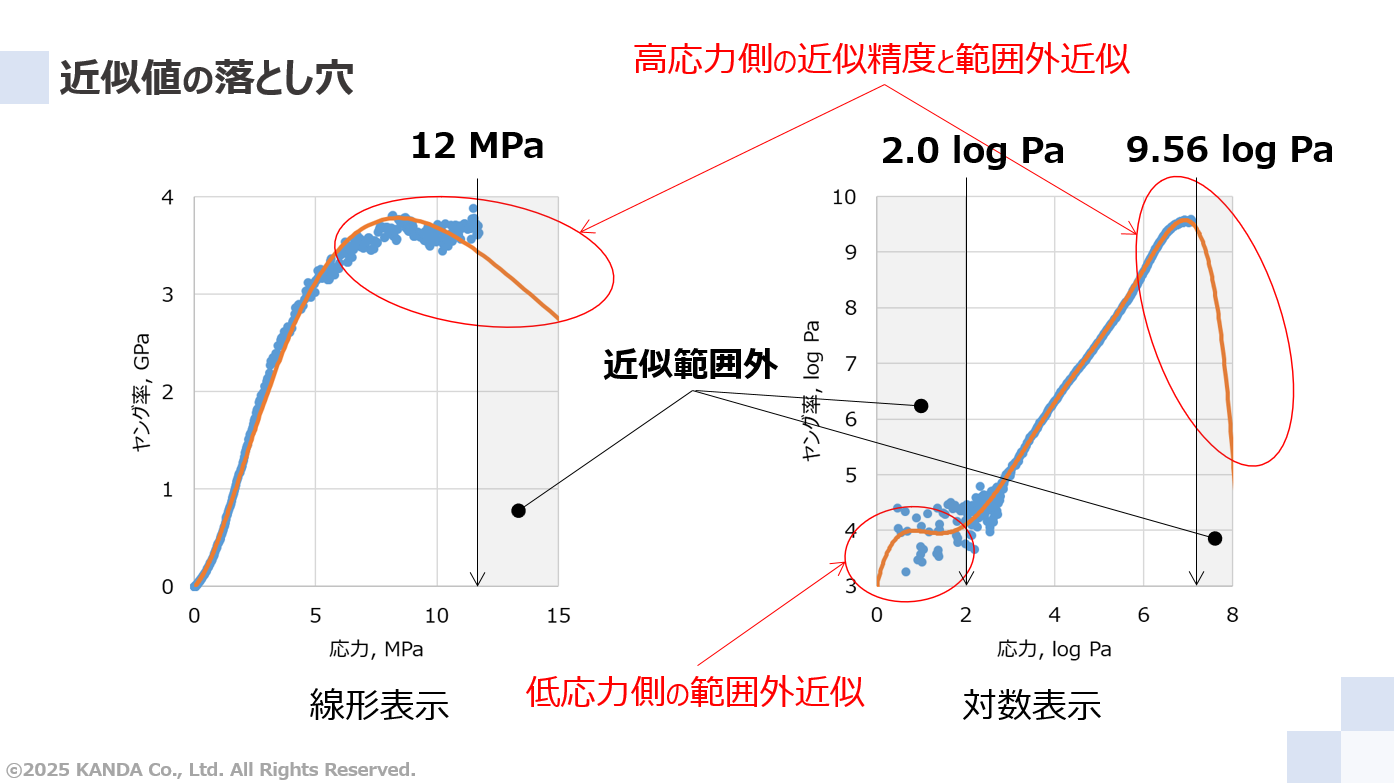
「近似式の選択とその近似精度」の対数多項式近似で示した圧縮ヤングの結果に対し、近似値の描画範囲を広くするとともに、測定値の近似範囲を描画した2つのグラフを示している。
いずれのグラフも高応力側の近似値は応力が高くなると低下する傾向であり、測定値のない近似範囲外の応力12MPa(=9.56 log Pa)以上で極端に低い値となる。つまり、この範囲の近似値は信頼性に欠ける。一方、測定値は応力が概ね7MPa以上で圧縮ヤング率が3.7GPa程度で一定になる傾向にある。
次に低応力側の近似値について考える。近似範囲の下限とした応力100Pa(=2 log Pa)は荷重で0.1N程度に相当する。それ以下ではロードセルの計測ノイズの影響が大きいために測定値が適切といえない。したがって、低応力側でも近似範囲外の近似値は信頼性に欠ける。
これらの結果を考慮し、次のように圧縮ヤング率の近似式に対処する。
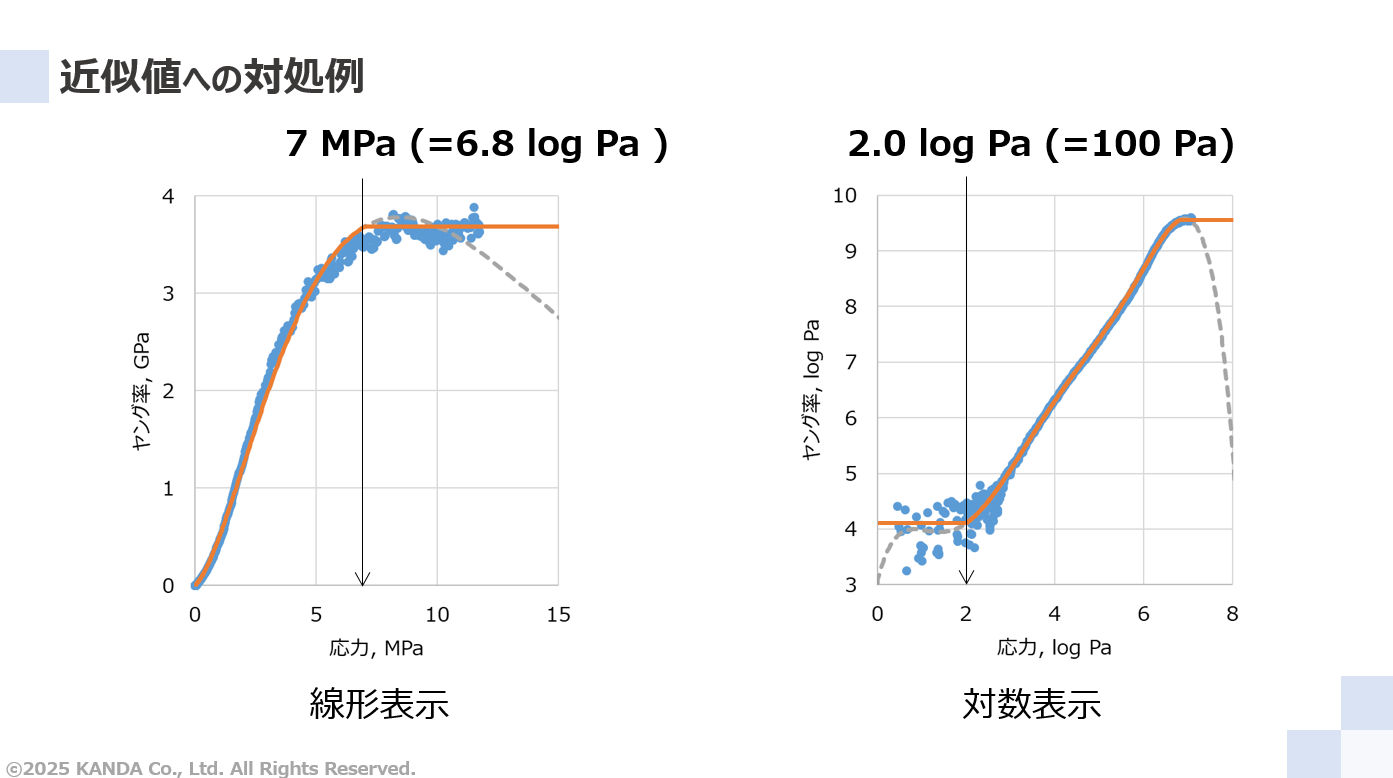
近似範囲外の近似値の信頼性、および応力が7MPa程度以上で測定値が一定になることに対し、臨界値を設けて対処する。低応力側を100Pa(=2.0 log Pa)、高応力側を7MPa(=6.8 log Pa)とし、より低い側とより高い側のヤング率の近似値を一定になるようにしている。2つのグラフともに臨界値で対処する前の近似値を灰色線、対処した後の近似値をオレンジ線で表している。
このようにして近似範囲外の問題を改善し、かつ近似精度を向上させることができる。
複合ウェブの圧縮ヤング率
異種材料を貼合したウェブや塗工層を設けたウェブといった複合ウェブについて、その圧縮ヤング率は複合ウェブそのもので試験・評価する。
複合ウェブの"引張ヤング率"は、複合ウェブそのものの引張試験、あるいは複合ウェブを構成する各層の引張試験の評価結果から算出することができた。しかしながら、圧縮ヤング率の場合は複合ウェブそのものの圧縮試験をする必要がある。この理由は「応力-ひずみ曲線の非線形性」で記載したように、圧縮ヤング率にはウェブ表裏の粗さ突起の潰れ具合が関係するためである。
巻取解析ソフトでの設定と計算結果例
巻取解析ソフトにおける半径方向ヤング率(圧縮ヤング率)の設定方法、および計算結果の例を示す。
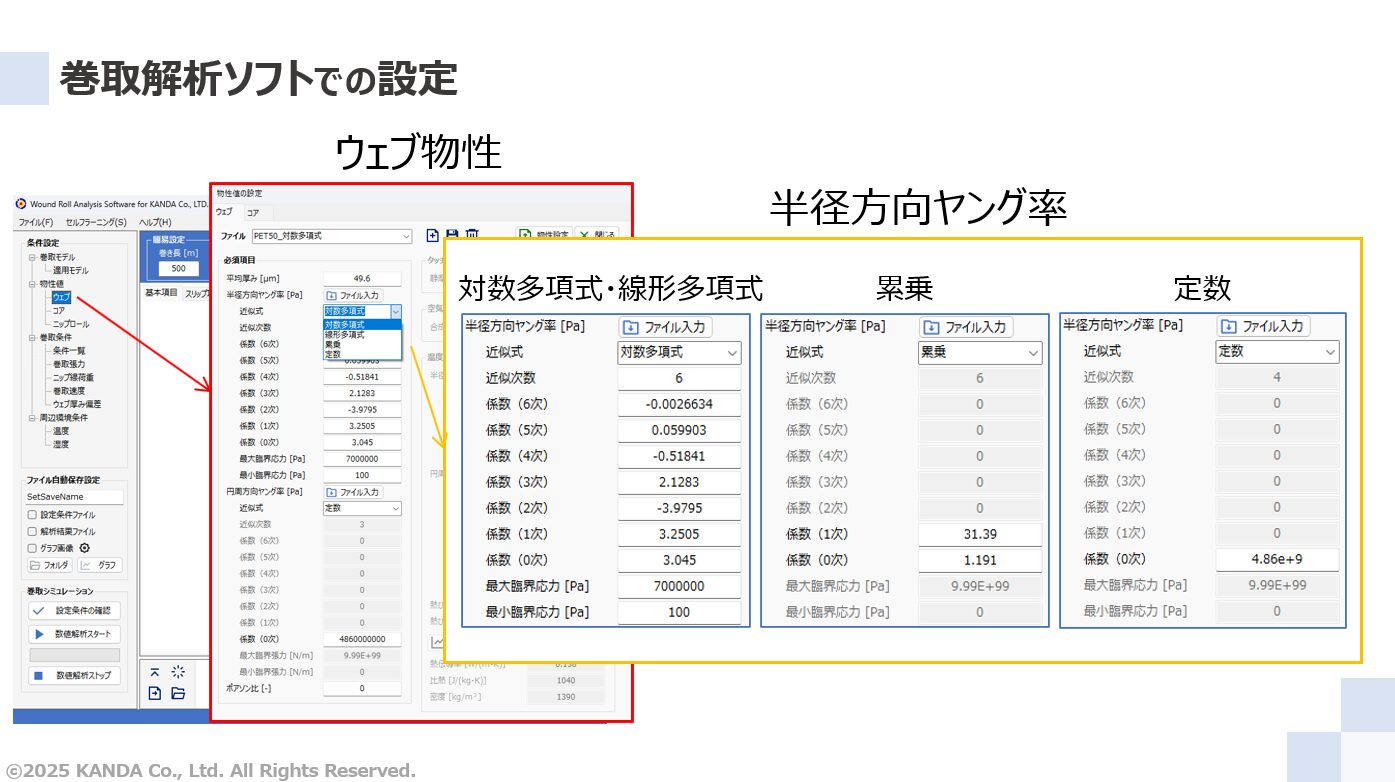
巻取解析ソフトのメイン画面における条件設定の「ウェブ」をダブルクリックすると、ウェブ物性の設定画面が表示される。この画面の必須項目の半径方向ヤング率における近似式のドロップダウンリストから「対数多項式」、「線形多項式」、「累乗」、「定数」のいずれかを選択して数値を入力する。
上述したPETフィルムを例に説明する。各近似における圧縮ヤング率は次のように表される。なお、巻取理論では圧縮ヤング率を半径方向ヤング率と称するため、これ以降は半径方向ヤング率と記載する。
【対数多項式近似】
![]()
【線形多項式近似】
![]()
【累乗近似】
![]()
【定数】
![]()
ここで、定数の場合は仮定を置いている。4.86×109は引張ヤング率と等しい、4.86×108は引張ヤング率の1/10倍になるとの仮定である。
次にドロップボックスで選択した項目に対応する半径方向ヤング率の設定方法を示す。
対数多項式あるいは線形多項式を選択した場合
半径方向ヤング率を対数多項式近似あるいは線形多項式近似した場合に選択する。画像は対数多項式を選択した状態である。
近似次数には近似した次数の6を入力し、各次数に対応した係数をそれぞれ入力する。次に「近似値の落とし穴と対処例」で示した臨界値である高応力側の7MPaと低応力側の100Paに対応させるため、最大臨界応力に7000000、最小臨界応力に100と入力する。臨界値の単位はいずれもPaである。
累乗を選択した場合
半径方向ヤング率を累乗近似した場合に選択する。係数(1次)に31.39、係数(0次)に1.191と入力する。
定数を選択した場合
半径方向ヤング率を一定とする場合に選択する。係数(0次)に設定する値を入力する。画像は4.86×109とした状態であり、4.86e+9と入力している。e+9は109を意味しており、4860000000と入力したのと同値である。
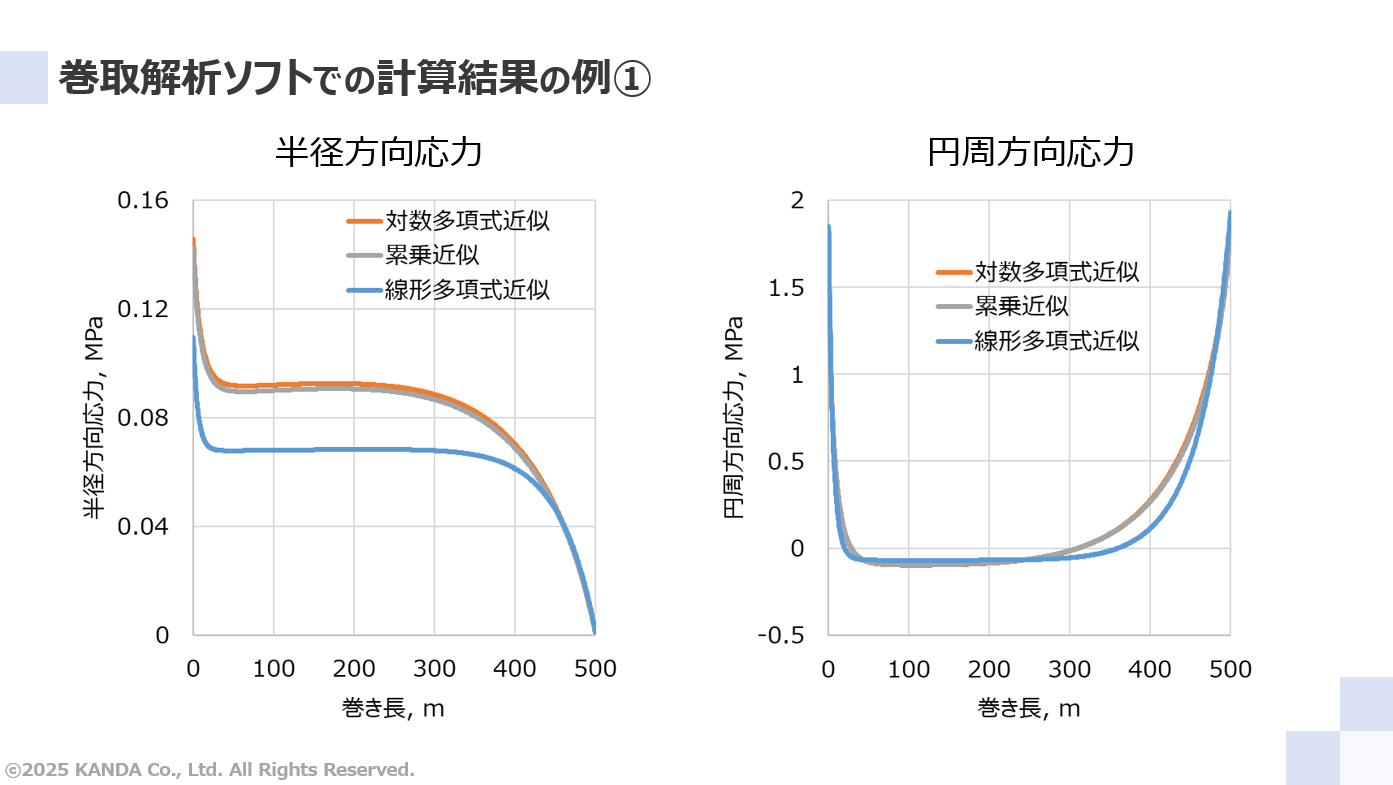
巻取解析ソフトをもちいて計算した理論予測値であり、左図は半径方向応力、右図は円周方向応力の結果である。それぞれ対数多項式と線形多項式と累乗の近似式による計算結果を示している。適用モデルはシンプルにHakielモデルとし、各種オプション(巻き込み空気の影響や温度変動の影響、ウェブ厚みムラの影響)は未考慮とした。また、巻取条件は張力を100N/m、巻き長を500mとしている。
上述したように、対数多項式が応力(ここでは半径方向応力のこと)とヤング率の関係の近似精度が広い範囲で最もよかった。したがって対数多項式近似の計算結果が最も理論予測の精度が高いといえる。これに対して、累乗近似はほぼ同じである一方、線形多項式近似は有意差が認められる。
計算結果の半径方向応力は0.1MPa(5 log Pa)オーダー以下である。この低応力側の近似精度は累乗近似で高く、線形多項式近似で低かった。これが計算結果に表れている。一方、累乗近似は高応力側の近似精度が良くなかった。つまり、半径方向応力が高くなる場合にはこの影響が反映される。
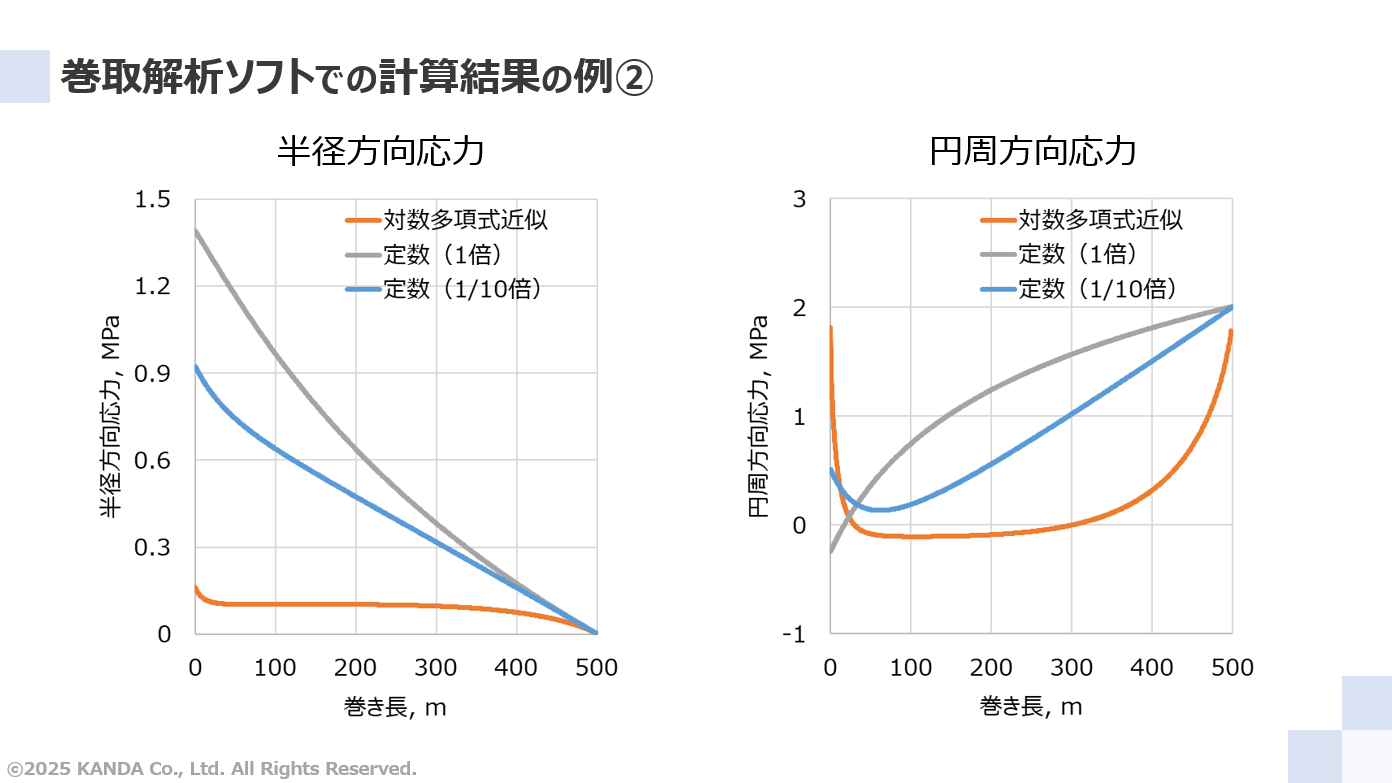
次に、半径方向ヤング率を定数とした場合の理論予測値を対数多項式近似の結果と比較したグラフを示している。
半径方向ヤング率を定数にするケースは、万能材料試験機や圧縮試験用治具を保有していないというように、圧縮試験の実施が困難な場合が多いだろう。このときは引張ヤング率のカタログ値、あるいは引張ヤング率よりも低い値が代用されている。
定数として引張ヤング率の1倍および1/10倍した値を半径方向ヤング率に設定している。いずれの理論予測値も半径方向ヤング率の近似精度の高い対数多項式の結果とは大きく異なる。
半径方向応力や円周方向応力の理論予測値はトラブル改善や安定生産を検討する指標として活用されるが、この予測精度が低いとミスリードにつながる恐れがある。
以上のことから、半径方向ヤング率を算出するために取得する圧縮試験データの信頼性、さらにデータ処理後の応力とヤング率の関係の近似精度をそれぞれ確保することは、巻取理論を実践に活用する上で非常に重要なことと言える。
半径方向ヤング率の受託評価サービスを行っている。希望される場合は「お問い合わせ」から相談いただきたい。
関連ページ
 ウェブハンドリング
ウェブハンドリング